planar 在三维空间中它是一个二维物体，有长和宽度，但没有厚度。一个真正的平面物体是不可以在三个方向上被扭曲的，一旦被扭曲，它就不再是平面。一个平面通过封闭曲线可以生成剪切面，但是这些曲线本身必须是平面曲线。 planars 在 maya 中生成文本时非常有用，实际上 trim 选项是为生成文本而设置的。
下面是一个关于平面物体的简单例子。画一个圆，同时通过选中该圆使其成为默认的平面，接着选择 surfaces → planar 命令得到一个剪切面，在圆上显示并选择一个 cv ，上下移动该 cv ，剪切圆的表面将消失，并且仅当 cv 恰好在基面上才出现，如图 4-50 所示。
(1) 建立一个新场景，执行 create → text 
命令，弹出 text curve options 窗口，在 text 文本框内输入 m ，更改 type 的类型为 trim ，如图 4-51 所示，单击 create 按钮，一个从字母 m 中抽取的平面曲线的轮廓就生成了。进入 persp 视图，可以在三维空间中看到平面曲线字母，你将看到如图 4-52 所示的图形。
图 4-51 text curve options 窗口中的设置
斜面几乎和平面相反，因为它实际上是使平整的东西产生厚度。但它很灵活而且功能强大，可以操作曲线和等参线，甚至是剪切边，生成斜面或斜边。
(2) 斜切上一步生成的字母 m 的平面外形。选择字母 m 曲线，选择 surface → bevel □。这里的选项因为具有方向性而可能产生混淆： top side( 斜切字母的背面 ) ； bottom side( 斜切前面 ) ； both( 斜切前面和后面 ) 。
提示：
当在 maya 中生成文本时，它是朝前的，如果不太理解 top 朝后、 bottom 朝前、 height 是挤压厚度的话，想象字母是面朝下躺在地面上即可。
可以使斜切角为 straight 或 circular ，让斜切边是直的、急剧的向内圆弧或光滑的向外圆弧。可以设置 bevel width 、 depth 和 height 为默认 —— 随后再适当地调整它们，单击 bevel 按钮，图形如图 4-53 所示。
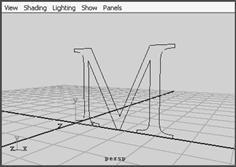
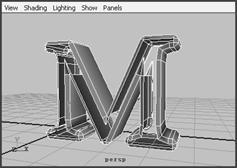
图 4-52 生成文字曲线 图 4-53 bevel 工具效果
如果要改变角和边的默认设置，可以打开 channel 盒，在 input 下单击 bevel1 可得到这些设置，按 t 键激活 show manipulator 得到 bevel 的历史记录，将看到 3 个和线相连的蓝色点。如果不想看到这些，可以选择 channel 盒，在 input 下再次单击 bevel1 ，它们就会消失。
(3) 这些蓝点是处理 bevel width 、 depth( 斜面或斜边的厚度 ) 或 height( 对文本曲线挤压的厚度 ) 的句柄。操作这些蓝点直到对字母 m 的形状满意为止，如图 4-54 所示，然后通过标记菜单显示物体的 isoparm 并选择斜面的前边。执行 surface → planar 命令，现在可以看到 m 的前面，如图 4-55 所示。
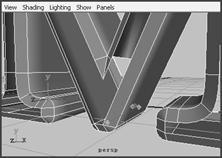
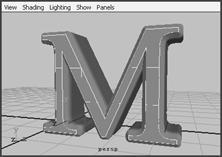
图 4-54 bevel 工具的操作器 图 4-55 最终形成的物体
边界
和放样曲线相比，边界的作用很容易描述，当两条曲线放样时，结果形成 4 条边的面，其中两条相对的边由曲线定义，另外两条通过计算两边之间的直线自动定义。当多于两条曲线放样时，另外两边被切割，但是在放样曲线之间它们是插进去的。相反，边界的作用是由 4 条曲线生成一个面的 4 条边，从而可以更好地控制面的边。
下面是 boundary 工具的工作方法。建立一个新的场景，每条曲线用两个或 3 个段生成 4 条不同的曲线，并把它们设置成终点相交，如图 4-56 所示。可以随便选择曲线，或框选所有曲线，但最先选择的曲线决定了边界面的 uv 参数化，因为曲线的自身 u 参数决定面的 u 参数，因此边界的 uv 方向是很重要的，应该记住所建立的最初的曲线。
一旦选中了所有的曲线以后，执行 surfaces → boundary 命令，并使用默认设置。这时应该有一个有 3 或 4 个 uv 段的表面，如图 4-57 所示。
图 4-56 4 条曲线的位置和形状 图 4-57 用 boundary 工具产生的表面
边界的另一个作用是可以用 3 条曲线形成一个表面。这种用边界建立的表面并不是一个真正的有 3 条边的表面，而应是一个有零长度边的表面。
[1] [2] 下一页
新闻热点
疑难解答
