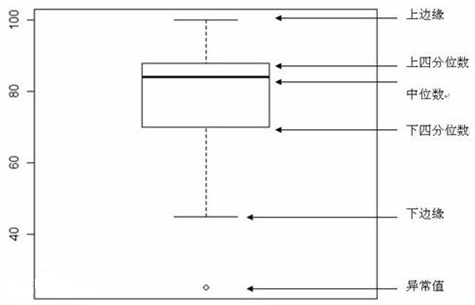
箱线图又称箱形图或盒须图,主要从四分位数的角度来描述数据的分布。一个箱线图由上边缘线、上四分位数(QU)、中位数(me),下四分位数(QL)和下边缘线组成。
上、下四分位数之差称为四分位差,或内距或四分位数间距,记为IQR:
IQR = QU - QL
箱线图中盒子的上、下线分别是上、下四分位数,盒子中间的线是中位数。由触须延长的上、下边缘线分别为:
上边缘线的值 = QU + 1.5 IQR下边缘线的值 = QL - 1.5 IQR
也有用数据的极大值和极小值来表示上下边缘线的值的(但使用这种表示上下边缘的方法无法检测异常值)。
一个箱线图的形式如下图所示:
箱形图为我们提供了识别异常值的一个标准:异常值被定义为小于QL-1.5IQR或大于QU+1.5IQR的值。虽然这种标准有点任意性,但它来源于经验判断,经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知,基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的,但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的,而均值和标准差的耐抗性极小,异常值本身会对它们产生较大影响,这样产生的异常值个数不会多于总数0.7%。显然,应用这种方法于非正态分布数据中判断异常值,其有效性是有限的。
箱形图的绘制依靠实际数据,不需要事先假定数据服从特定的分布形式,没有对数据作任何限制性要求,它只是真实直观地表现数据形状的本来面貌;另一方面,箱形图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的耐抗性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响,箱形图识别异常值的结果比较客观。由此可见,箱形图在识别异常值方面有一定的优越性。(以上两段来自百度百科-箱形图)
在R语言中绘制箱线图使用boxplot函数,该函数的使用方法,可以参见本站《R语言中绘制箱线图》。
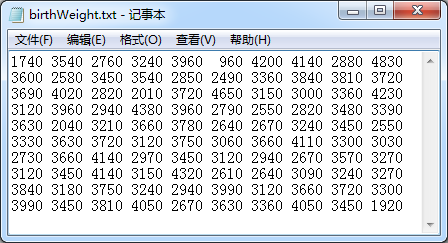
我们仍然使用《标准分数法检测数据的异常值及在R语言中的实现方法》这篇文章中的例子。数据存储在文本文件中(下载数据: 点击下载此文件),数据存储格式如下图所示:
点击下载此文件),数据存储格式如下图所示:
编写R语言:
x <- scan("birthWeight.txt") # 定义变量X读取数据
names(x) <- 1 : length(x) # 给每个数据编号
boxplot(x) # 绘制箱线图
out.vals = boxplot(x)$out # 获取异常值信息
print(out.vals) # 输出异常值信息
for( i in out.vals) # 在图上标注异常点的值
{
text(i, adj = -0.2, labels = i)
}
输出结果及绘图结果如下面靓图所示:

从输出结果可以看出,编号为1和6的两个数据为异常点。
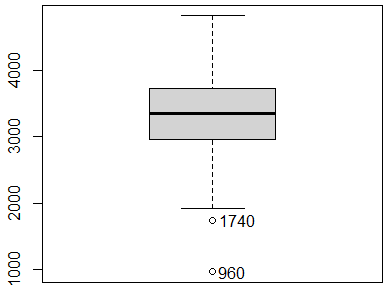
从绘图结果来看,有两个点属于异常点,其位于箱线图下边缘线以下,属于异常小离群点,图中也标注了其具体的值为1740和960。
新闻热点
疑难解答