均匀分布及在R语言中的实现

均匀分布也称矩形分布，是最简单的一种连续型分布。

一、均匀分布

若随机变量X的概率密度函数为：

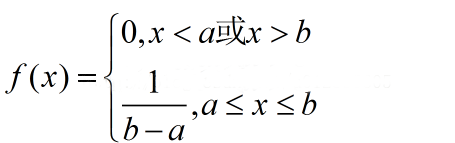
则称X服从区间[a, b]上的均匀分布，记为X~U[a, b]。

概率密度图像如下图所示：

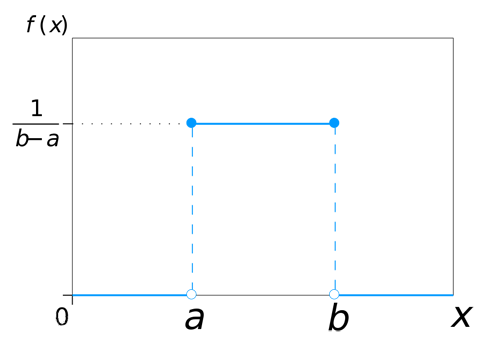
其分布函数为：

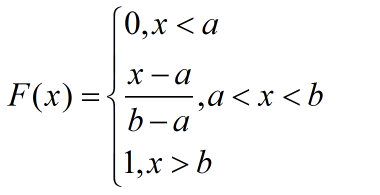
分布函数是概率密度函数从负无穷到正无穷上的积分；在坐标轴上，概率密度函数的函数值y表示落在x点上的概率为y；分布函数的函数值y则表示x落在区间(-∞，+∞）上的概率。

分布函数图像如下图所示：

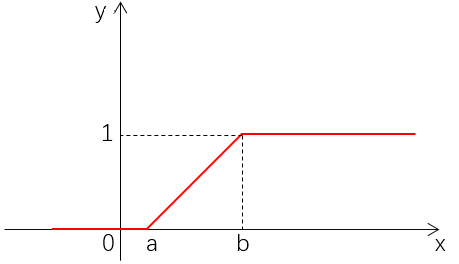
均匀分布的数学期望与方差分别为：

二、R语言与均匀分布相关的函数

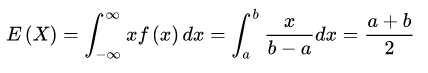
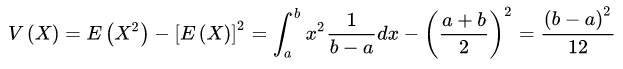
在R中，unif是用来进行均匀分布分析的，在其前面加上不同的前缀表示不同的函数，各函数的使用格式如下所示：

dunif(x, min = 0, max = 1, log = FALSE)  # 分布密度
punif(q, min = 0, max = 1, lower.tail = TRUE, log.p = FALSE)  # 分布函数
qunif(p, min = 0, max = 1, lower.tail = TRUE, log.p = FALSE)  # 分位数函数
runif(n, min = 0, max = 1)  # 随机数产生函数

各参数的主要含义如下：

x, q ： 数值向量

p ： 概率向量

n ： 观测次数值

min, max ： 均匀分布的下限和上限，必须是有限的值，min相当于密度函数或分布函数中的a，默认值为0，max相当于b，默认值为1；

log, log.p： 逻辑值，默认为FALSE.指定为TRUE时，概率值p是以log(p)给出的；

lower.tail ： 逻辑值，默认为TRUE. 指定为TRUE时，概率是P [ X ≤ x ]，否则是 P [ X ＞ x ].

三、均匀分布使用案例

设电阻R是随机变量，其值均匀分布在900Ω~1100Ω。

（1）求该区间内的分布密度；

（2）求电阻不超过950Ω的概率；

（3）求电阻超过950Ω的概率；

（4）在90%概率下，电阻值最大为多少；

（5）随机生成5个符合该均匀分布的电阻值。

由题意可知：其分布函数 f(r) = 1/(1100-900) = 1/200 ( 900 ≤ r ≤ 1100）

（1）因为是均匀分布，使用R语言进行求值时，选取[900, 1100]中任何一个值，其概率密度值都是一样的。

（2）即求 P(r ≤ 950)的概率，使用分布函数可以方便求出；

（3）即求p(r>950)的概率，可以使用 1 - p(r≤950) 计算得出。

（4）实际上相当于“电阻值不大于r的概率是90%，求x”，可以使用分位函数来求；

（5）使用runif()函数可以获得这样的随机值。

编写R程序如下：

a <- 900
b <- 1100

# 计算概率密度
f <- dunif(900, a, b) 
cat("概率密度为：", f, "/n")

p <- punif(950, a, b)
cat("电阻不超过950欧姆的概率为：", p, "/n")

p <- 1 - punif(950, a, b)
cat("电阻超过950欧姆的概率为：", p, "/n")

R <- qunif(0.9, a, b)
cat("90%概率下，电阻值最大为：", R, "/n")

# 随机生成5个符合该均匀分布的随机电阻值
runif(5, a, b)

在R运行结果如下图所示：

本文（完）