泊松分布及在R语言中的实现

泊松分布（Poisson Distribution）是一种离散型概率分布。泊松分布是描述某一特定时间或空间段内，某一事件发生的次数的分布。如机器每周发生故障的次数，某医院妇产科2小时内出生的婴儿个数，某服务台在某时间段内到达的顾客次数等。

一、泊松分布律

泊松（Poisson）分布的分布律为：

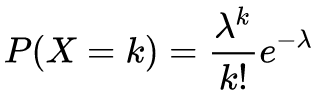
其中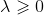，则称X服从参数为的泊松分布，记为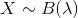或。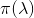

这里的P即为等同区间内事件发生k次的概率；

X：事件次数的变量；

k:事件发生的次数，取值为0,1,2,3...

λ：区间内事件发生的平均次数（数学期望）

同时，显然有：

二、泊松分布的数学期望与方差

三、适用条件

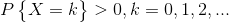
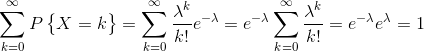
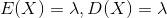
（1）事件发生是小概率事件；

（2）事件的发生是相互独立的；

（3）事件在任意两个等同的区间内发生的概率是稳定的。

四、泊松分布的特征

（1）泊松分布是一种描述和分析稀有事件的概率分布。要观察到这类事件，样本含量n必须很大。

（2）λ是泊松分布所依赖的唯一参数。λ值愈小，分布愈偏倚，随着λ的增大，分布趋于对称。

（3）当λ = 20时，泊松分布接近于正态分布；当λ = 50时，可以认为泊松分布呈正态分布。在实际工作中，当λ≥20时就可以用正态分布来近似地处理泊松分布的问题。

五、R语言中的相关函数与实例

1、相关函数

在R中，pois表示泊松分布，加上不同的前缀表示不同的函数，加上前缀d表示概率密度函数，加上前缀p表示分布函数，加前缀q表示分位函数，加前缀r表示随机生成数，各函数的语法格式如下：

dpois( x, lambda, log = FALSE )   #发生x次随机事件的概率

ppois( q, lambda, lower.tail = TRUE, log.p = FALSE ) # 至多发生q次事件的累计概率

qpois( p, lambda, lower.tail = TRUE, log.p = FALSE ) #在p概率下事件发生的次数

rpois( n, lambda ) #重复n组试验，每组发生随机事件的次数

函数中各参数的含义：

• x ：非负整数向量，事件发生的次数；
• q：数值向量；
• p：概率值向量
• n：整数值，随机试验的次数；
• lambda：非负数值，事件发生的平均次数；
• log,log.p：逻辑值，如果为TRUE，则概率p以log(p)的形式给出
• lower.tail：逻辑值，如果为TRUE（默认值），则概率是p[x≤ x],若为 FALSE 则为p[X>x]。

几点说明：

（1）若x为非整数，dpois 的结果将会使0，并给出一个警告错误；

（2）分位数是右连续的，qpois(p, lambda) 表示x是最小整数的情况：P(X ≤ x) ≥ p；

（3）设置lower.tail = FALSE，可以得到更加精确的结果，而lower.tail = TRUE将返回1；

（4）无效的lambda值，将会返回NaN，并给出警告错误。

2、使用示例

（1）某银行，顾客到达柜台的平均值是5分钟3.2名，计算：①接下来5分钟内，有0名顾客、1名顾客和2名顾客到达的概率分别是多少？②在5分钟内至多有7名顾客到达的概率是多少？③在5分钟内有7名以上顾客到达的概率是多少？④在90%的概率下，5分钟内至多有几名顾客到达？

编写R程序如下：

lmbda <- 3.2
# 5分钟内0名、1名、2名顾客的概率
dpois(0:2, lmbda)

# 5分钟至多7名顾客的概率
ppois(7, lmbda)

# 5分钟有7名以上顾客到达的概率
1 - ppois(7, lmbda)

# 90%概率下，5分钟内至多有几名顾客到达
qpois(0.9,  lmbda)

运行结果如下图所示：

（2）某工厂某种设备每周的平均故障台数为2.3台，求下周该设备没有发生故障的概率，下周至多有3台发生故障的概率；重复模拟10组试验，每组发生故障的台数是多少

编写R程序如下：

lambda <- 2.3
# 下周没有设备发生故障的概率
dpois(0, lambda)

#下周至多有3台设备发生故障的概率
ppois(3, lambda)

#重复1000组试验，每组发生故障的台数
rpois(10, lambda)

在R中运行的结果如下图所示：

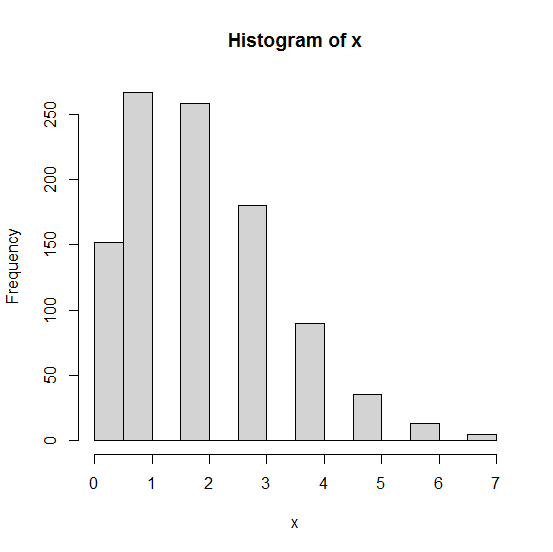
我们也可以使用R绘制出泊松分布的概率密度图，下例演示了均值为2，重复1000次情况下的直方图。

x <- rpois(1000, 2)
hist(x)

绘图结果之一如下（因为随机生成，每次的结果并不一定相同）：

本文（完）