标准分数法检测数据的异常值及在R语言中的实现方法

一、异常值的概念

在数据处理与应用中（如训练机器学习算法或应用统计技术），错误值或异常值通常会造成测量误差或异常系统条件的结果。

有时数据集中含有一个或多个异常大或者异常小的观测值，像这种极端的值被称为异常值。通常异常值产生的原因可能有：

（1）观测、记录或录入时不正确；

（2）测量值来自不同的总体；

（3）测量值是正确的，但代表一个稀有或偶然的事件。

二、异常值的判断之标准分数法

目前有许多技术可以检测异常值，并且可以自主选择是否从数据集中删除。

这篇文章首先介绍一下一维数据中检测异常值的一个方法：标准分数法。

变量值与其平均数的差除以标准差的值称为标准分数，或称Z得分，公式如下：

当Z_i的绝对值大于某个数值时，可以将第i个样本看成异常值。

三、异常值判断法则

在具体使用时，可以使用下面的判别法则。

（1）经验法则：若数据集近似于丘形对称分布，则①大约有68%的测测量值位于平均值的1个标准差的范围内；②大约有95%的测量值位于平均值的2个标准差的范围内；③几乎所有的测量值位于平均值的3个标准差的范围内。

（2）切比雪夫法则：对于任意的数据集，无论数据的频数分布是什么形状的，则①可能有很少的测量值落在平均值落在平均值的1个标准差的范围内；②至少有3/4的测量值落在平均值的2个标准差的范围内；③至少有8/9的测量值落在平均值的3个标准差的范围内；④对于任意大于1的数k，至少有1-1/k₂的测量值落在平均值的k个标准差的范围内。

通过z得分及这两个法则，可以判断哪些样本是异常的。

四、标准分数法在R语言中实现的方法

这里使用一个具体的例子来说明标准分数法的具体使用过程。

某妇产医院随机地选取了100个新生儿，其体重数据存储在名为birthWeight的文本文件中。找出这些新生儿体重的异常值。数据在文件中的存储格式如下：

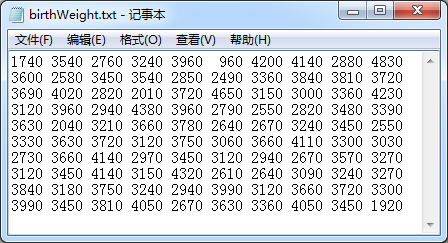
编写R语言程序：

X <- scan("birthWeight.txt") #定义变量X读取数据
names(X) <- 1:length(X) #给每个数据编号
Xjz <- mean(X) #均值
S <- sd(X) #标准差
Z <- (X - Xjz) / S #Z得分
X[abs(Z) > 3] #提取出得分绝对值大于3的值

其在R语言编辑器中的情景：

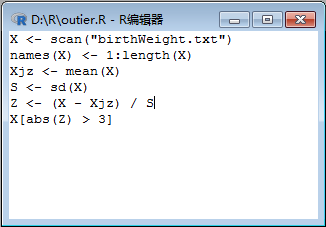
运行结果如下图所示：

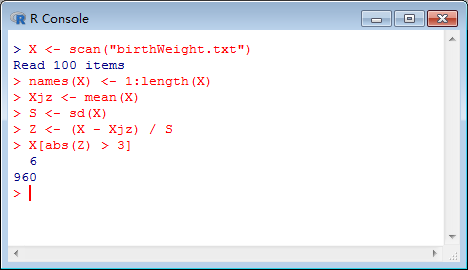
从运行结果来看，是第6个数据960属于异常值。因为根据经验法则来看，几乎所有的观测值Z得分的绝对值均小于3.