伯努利分布、二项分布及在R中的实现

1、伯努利分布

在我们实际生活中，许多事件发生的结果存在着非此即彼的现象，如抛硬币，正面朝上的结果不是“是”就是“否”，或“正”或“反”；出生婴儿的性别一般是“男”或“女”，抽奖的结果不是“中了”就是“没中”等。这些事件可以被称为伯努利实验。

伯努利分布(Bernoulli distribution)又名两点分布或0-1分布。伯努利分布是一个离散型的随机分布，其中的随机变量只有两类取值。伯努利试验是单次随机试验，只有"成功（值为1）"或"失败（值为0）"这两种结果，是由瑞士科学家雅各布·伯努利(1654 - 1705)提出来的。

伯努利试验是只有两种可能结果的单次随机试验，即对于一个随机变量X而言：

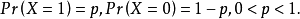
则称随机变量X服从参数为p的伯努利分布，若令q=1一p，则X的概率函数可写为：

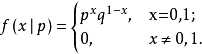
或：

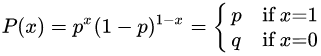
其期望值为：

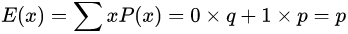
其方差为：

2、二项分布

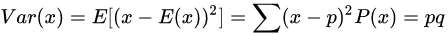
二项分布(Binomial distribution)即重复n次的伯努利试验，记为 X~b(n,p)。概率密度函数（概率质量函数）为

其中，

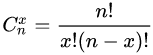
是组合公式，表示从n个不同元素中取出x个元素的所有组合的个数。其中n是试验次数，x是试验结果为正的次数，q是试验结果为正的概率，1-q是试验结果为负的概率。

显然，从定义可以看出，伯努利分布是二项分布在n=1时的特例.

其期望为：

μ = np

方差为：

σ²=npq

3、R语言中的相关函数

（1）dbinom(x, size, prob) 试验size次，每次成功率为prob，成功x次的概率是多少？

（2）pbinom(q, size, prob) 成功q次的累计概率

（3）rbinom(n, size, prob) 返回n个试验size次的成功次数

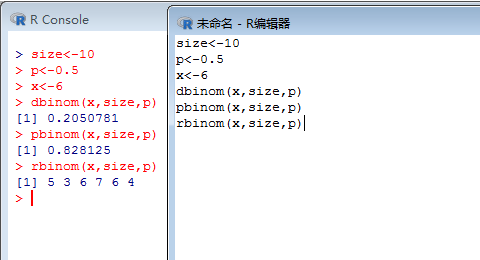
假设玩抛硬币游戏，共抛10次，每次正面朝上（成功）的概率为0.5，

size <- 10
p <- 0.5
x <- 6
dbinom(x, size, p)
pbinom(x, size, p)
rbinom(x, size, p)