使用R语言进行有交互作用的双因素方差分析

在前面文章中介绍了双因素方差分析的相关知识以及无交互作用的双因素方差分析的相关理论，并给出了R语言的相关代码。本文将进一步介绍一下有交互作用的双因素方差分析方法，并在R中实现的基本方法。

关于无交互作用的方差分析方法，可参见本站的文章：使用R语言进行无交互作用的双因素方差分析

在实际中，两个因素往往对要研究的问题存在着交互影响，如适当的施肥量和降雨量对农作物的产量存在着交互影响。

有交互作用的方差分析表如下图所示：

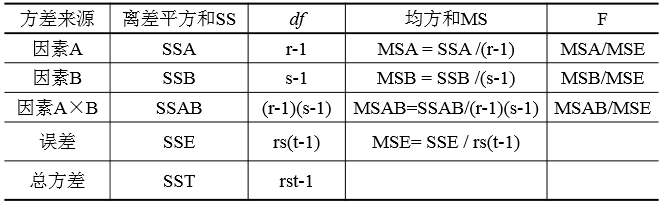
为检验因素A的影响是否显著，采用统计量：

为检验因素B的影响是否显著，采用统计量：

为检验因素A、B交互效应的影响是否显著，采用统计量：

R语言中进行有交互作用的双因素方差分析的方法

在R语言中，有交互作用的双因素方差分析方法与无交互作用的双因素方差分析所使用的函数相同，即aov函数和summary函数。

下面举例子来说明：

例1：电池的板极材料与使用的环境温度对电池的输出电压均有影响。

今材料类型与环境温度都取了三个水平，测得输出电压数据如下表，问不同材料、不同温度及它们的交互作用对输出电压有无显著影响(α=0.05)，数据如下图所示：

本例的数据保存在文本文件中，每个数据以空格隔开，有兴趣的读者可以点击下面的链接进行下载实验。

本例的数据文件下载（请右击选择连接另存为）：点击下载此文件

在R中编写程序如下：

#####有交互作用的方差分析

#使用scan函数从文本文件中读取数据
V<-scan("vmt.txt") 

#定义材料因子
M<-gl(3,12,labels=c("M1","M2","M3"))

#定义温度因子
T<-gl(3,4,labels=c("T1","T2","T3")) 

#定义数据框
VMT<-data.frame(V, M, T) 

#进行分析
fx<-aov(V~M+T+M:T, data=VMT) 

summary(fx) #提取方差分析表

在上面的方差分析函数aov中，第一个参数使用了公式的形式：V~M+T+M:T，其中M:T表示两个因素间的交互作用，如没有这一项，则表示因素M和因素T的无交互作用的方差分析。

其运行结果如下：

从上图的结果来看，材料因素的Pr=0.004<0.05，则说明材料对输出电压的影响具有显著性区别，温度因素的pr=1.52e-09<0.05，则说明温度对输出电压的影响非常显著，M:T即材料和温度的交互作用的pr=0.0008<0.05，说明两者的交互作用对输出电压的影响也是显著的。

例2：不同教学方法和教材对学习效果是否有影响。

用三种不同教材和两种不同教学方法在6个小班重复实验得到的数据如下：

问：教材，教法及两者的交互作用是否对教学效果有影响。

教学效果的数据存储在jxxg.txt文件中，以英文逗号(,)作为分隔符。可以点击下面的链接进行下载：

教学效果数据文件下载（请右击选择连接另存为）：点击下载此文件

在R中编写程序如下：

########有交互作用的方差分析
##教学方法和教材对教学效果的影响分析##

#从jxxg.txt文件中读取数据
#每个数据以英文逗号(,)作为分隔
eff<-scan("jxxg.txt",sep=",")

#定义教材因子
jc<-gl(3,8,labels=c("B1","B2","B3"))

#定义教法因子
jf<-gl(2,4,length=24,labels=c("M1","M2"))

#定义数据框
JXXG<- data.frame(eff,jc,jf)

#进行方差分析
aova.double<-aov(eff~jc+jf+jc:jf,data=JXXG)

#提取方差分析表
summary(aova.double)

运行结果如下图所示：

从上图可以看出，jc（教材）因素和jf（教法）因素分别对教学效果有显著影响，而两者的交互作用对教学效果的影响不够显著。