双因素方差分析就是考虑两个因素的方差分析,两个因素可以称之为因素A和因素B,设因素A有r个水平A1,A2,...,Ar,因素B有s个水平B1,B2,...,Bs.
双因素方差分析有两种类型:
一种是无交互作用的双因素方差分析,它假定因素A和因素B的效应之间是相互独立的,不存在相互关系;
另一种是有交互作用的方差分析,它假定A、B两个因素不是独立的,而是相互起作用的,两个因素同时起作用的结果不是两个因素分别作用的简单相加,两者的结合会产生一个新的效应。
这种效应的最典型的例子是,耕地深度和施肥量都会影响产量,但同时深耕和适当的施肥可能使产量成倍增加,这时,耕地深度和施肥量就存在交互作用。两个因素结合后就会产生出一个新的效应,属于有交互作用的方差分析问题。
本文首先探讨一下无交互作用的双因素方差分析相关问题。
无交互作用的双因素方差分析的数据结构表如下:
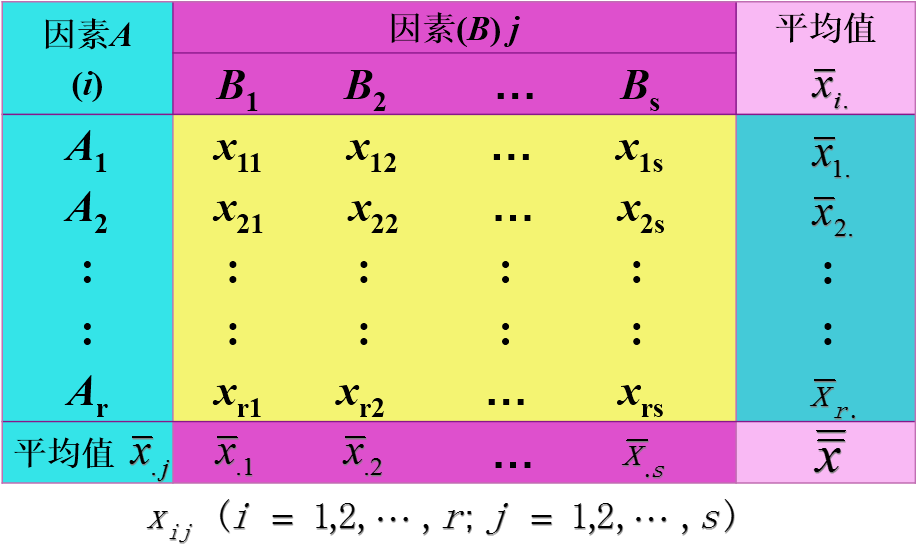
分析的步骤
(1)提出假设
对因素A提出的假设为:
H0: μ1 = μ2 = … = μi = …= μr (μi为第i个水平的均值)
H1: μi (i =1,2, … , r) 不全相等
对因素B提出的假设为:
H0: μ1 = μ2 = … = μj = …= μs (μj为第j个水平的均值)
H1: μj (j =1,2,…,s) 不全相等
(2)构造检验统计量
总离差平方和:
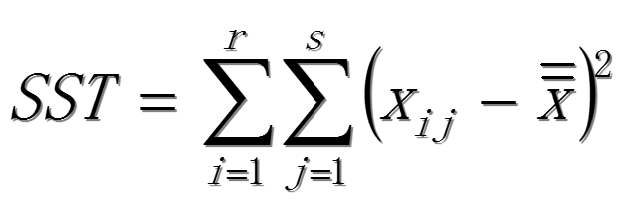
因素A的离差平方和SSA:
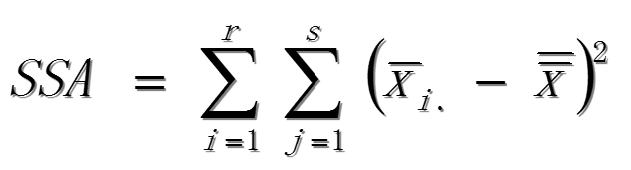
因素B的离差平方和SSB:
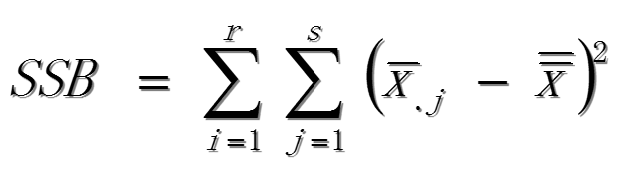
误差项平方和SSE:
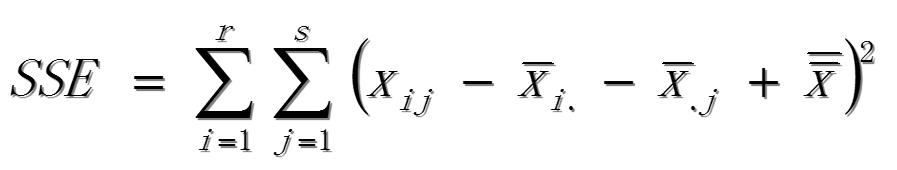
各平方和的关系:
SST = SSA + SSB + SSE
(3)计算均方MS
因素A的均方:
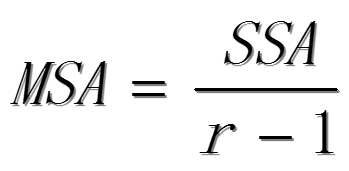
因素B的均方:
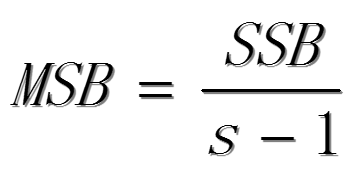
随机误差项的均方:

(4)计算检验统计量F

(5)统计决策
将统计量的值F与给定的显著性水平α的临界值Fα进行比较,作出接受或拒绝原假设H0的决策:
根据给定的显著性水平α在F分布表中查找相应的临界值 Fα
若FA≥ Fα,则拒绝原假设H0,表明均值之间的差异是显著的,即所检验的因素(A)对观察值有显著影响
若FB≥Fα,则拒绝原假设H0,表明均值之间有显著差异,即所检验的因素(B)对观察值有显著影响
无交互作用的方法分析表如下:
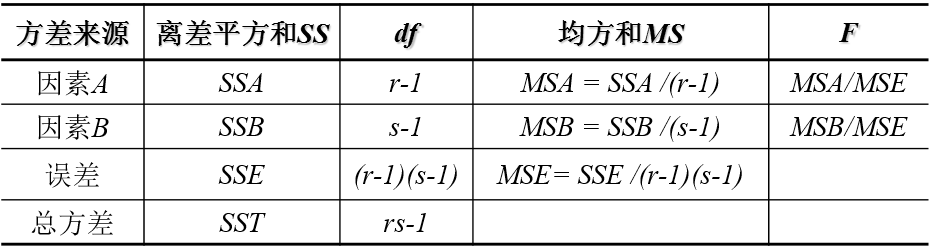
R语言中进行无交互作用的双因素方差分析的方法
在R语言中,无交互作用的双因素方差分析方法与单因素方差分析所使用的函数相同,即aov函数和summary函数。
下面举例子来说明:
例1:某产品销售量是否与销售方式和销售地点有关
某公司想知道产品销售量与销售方式及销售地点是否有关,随机抽样得表中资料,以0.05的显著性水平进行检验。
| 地点一 | 地点二 | 地点三 | 地点四 | 地点五 | |
| 方式一 | 77 | 86 | 81 | 88 | 83 |
| 方式二 | 95 | 92 | 78 | 96 | 89 |
| 方式三 | 71 | 76 | 68 | 81 | 74 |
| 方式四 | 80 | 84 | 79 | 70 | 82 |
在R中编写程序如下所示:
#无重复作用的双因素方差分析
#定义销售量向量
X<-c(77,86,81,88,83,95,92,78,96,89,71,76,68,81,74,80,84,79,70,82)
A<-gl(4,5) #销售方式四种
B<-gl(5,1,20) #销售地点五个
sales<-data.frame(X,A,B) #创建数据框
sales.aov<-aov(X~A+B,data =sales)
summary(sales.aov)
运行结果如下图所示:
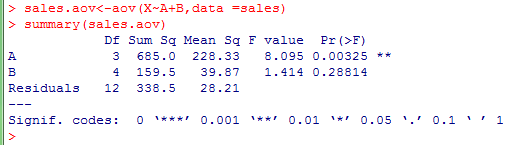
从分析结果来看,销售方式的P值=0.00325<0.05,则认为因素A不同销售方式对销售量有显著影响,而销售地点的P值=0.28814>0.5,没有充分理由说明销售地点对销售量有影响。
例2:食品包装和销售地区对某商品销售量是否有影响
为研究食品的包装和销售地区对其销售量是否有影响,在某周的三个不同地区中用三种不同包装方法进行销售,获得的销售量数据如下表。
| 销售地区(A) | 包装方法(B) | |||
| B1 | B2 | B3 | B4 | |
| A1 | 45 | 75 | 30 | 40 |
| A2 | 50 | 50 | 40 | 48 |
| A3 | 35 | 65 | 50 | 53 |
检验不同的地区和不同的包装方法对该食品的销售量是否有显著影响? (α=0.05)
在R中编写程序如下:
X<-c(45,75,30,40,50,50,40,48,35,65,50,53)
A<-c(1,1,1,1,2,2,2,2,3,3,3,3)
#或者A<-gl(4,4)
B<-rep(c(1:4),3)
#或者B<-gl(4,1,12)
dat<-data.frame(X,A,B)
re<-aov(X~A+B,data=dat)
summary(re)
分析结果如下:
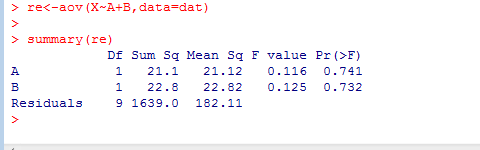
从分析结果来看,因素A和因素B的P值均大于0.05,则可以认为因素A和因素B对食品销售量没有影响。
新闻热点
疑难解答