1、什么是相关关系
相关分析(correlation analysis),从数量上分析现象之间相关关系的理论和方法。
现象之间的关系可以分为确定关系和非确定性关系。
确定性关系,可以说是函数关系,也就是说对于某一变量的每个数值都有另一变量的完全确定的值与之对应。
非确定性关系,即这里所说的相关关系,现象之间存在一定的依存关系,但不是一一对应的关系,即相随变动关系。
我们这里探讨的就是相关分析。
2、相关关系的分类
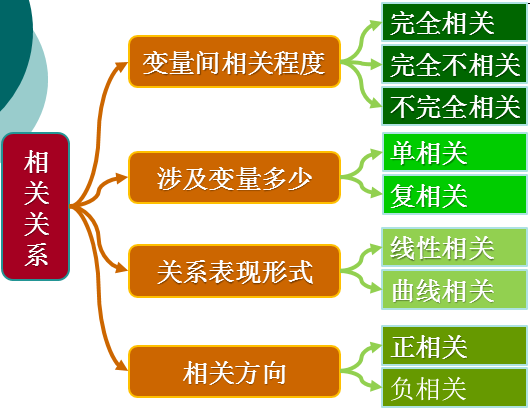
这篇文章主要研究线性相关关系
3、相关分析的基本步骤
(1)绘制散点图,初步判断两个变量之间是否存在某种(线性)有规律的变化;
(2)正态性检测,如要选择Pearson相关系数,则要判断两个变量是否服从正态分布或近似正态;
(3)计算相关系数,选择相关的方法公式来计算两个变量的相关系数r;
(4)显著性检验,判断这种相关性是否显著;
(5)给出结论。
4、散点图
散点图可以在坐标系中表示因变量随自变量而变化的大致趋势,据此可以选择合适的函数对数据点进行拟合。在R中绘制散点图的方法可以参加本站中的另外一篇文章:《使用R语言绘制散点图》
下图的散点图表示了两个变量之间可能的情况:
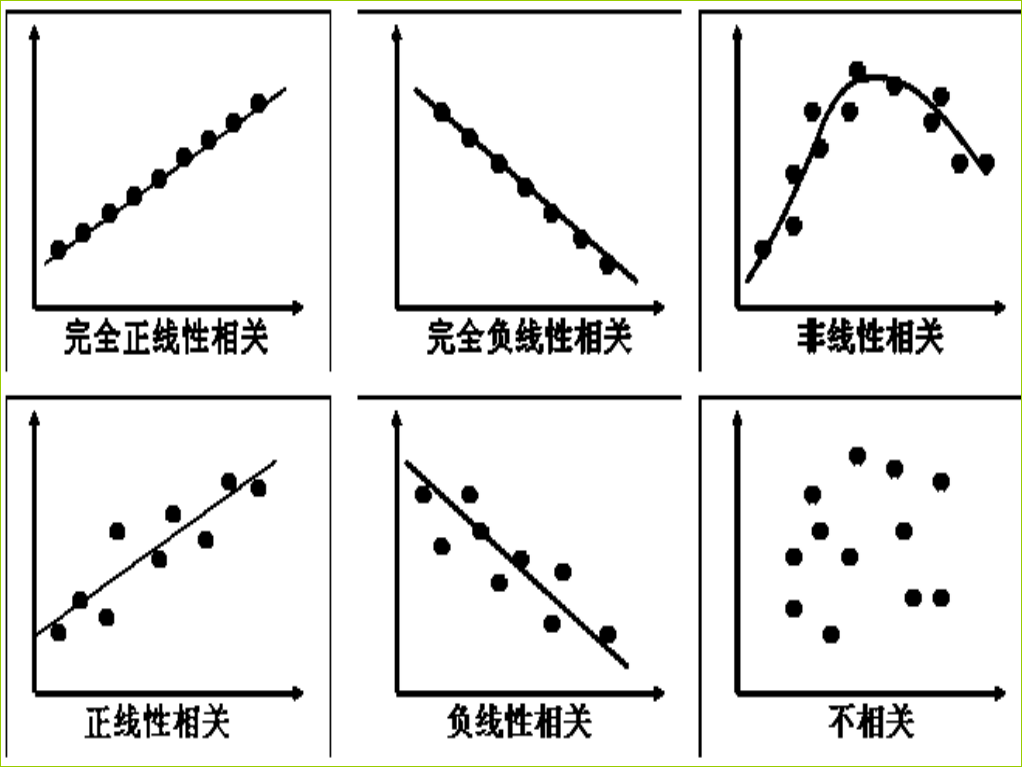
5、相关系数
相关系数(CorrelationCoefficient),是专门用来衡量两个变量之间的线性相关程度的指标,经常用字母r来表示相关系数。
(1)Pearson相关系数
最常用的相关系数,是皮尔逊(Pearson)相关系数,又称积差相关系数,其公式如下:

(2)Spearman相关系数
用于两个定序或定类变量的相关程序,对数据分布形态不作要求,也可以用于定序数据,但不如Pearson精确。
秩相关系数的计算步骤如下:
1)把数量标志和品质标志的具体表现按等级次序编号;
2)按顺序求出两个标志的每对等级编号的差;
3)按下式计算相关系数:
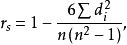
其中:秩相关系数记为rs,为两变量每一对样本的等级之差,即变量xi与yi的差值,n为样本容量。
秩相关系数与相关系数一样,取值-1到+1之间,rs为正时表示正相关,rs为负时表示负相关,rs等于零时表示相关为零。但与相关系数不同的是,它是建立在等级的基础上计算的,较适用于反映序列变量的相关。
(3)Kendall相关系数
用于反映分类变量一致性的指标,两个变量均属于有序分类时使用,Kendall相关系数将在本站另行探讨。
相关系数r主要特征有:
(1)取值范围在[-1,1]之间。
(2)|r|越趋于1,表示线性相关越强;|r|越趋于0,表示线性相关越弱。
(3)若|r|=1,为完全线性相关(相当于两变量是确定的函数关系)
(4)若r >0,表示两个变量存在正相关,若r<0,表示两个变量存在负相关,若r = 0,表示两个变量不存在线性相关关系。
在实际中,将r分成几个区间段来表示两个变量之间的相关强度:
(1)|r|<0.3 相关极弱,为不存在线性相关关系;
(2)0.3 ≤ |r| < 0.5 为低度(弱)线性相关;
(3)0.5 ≤ |r| <0.8为中度(显著)线性相关;
(4)|r| ≥0.8为高度线性相关。
相关分析与回归分析在实际应用中有密切关系。然而在回归分析中,所关心的是一个随机变量Y对还有一个(或一组)随机变量X的依赖关系的函数形式。而在相关分析中 ,所讨论的变量的地位一样,分析侧重于随机变量之间的种种相关特征。比如,以X、Y分别记小学生的数学与语文成绩,感兴趣的是二者的关系怎样,而不在于由X去预测Y。
在R中可以使用cor函数计算两组变量之间的相关系数。cor()函数的形式如下:
cor(x, y = NULL, use = "everything", method = c("pearson", "kendall", "spearman"))
其中,x为数值向量、矩阵或数据框;y默认为NULL值,其为与x具有相同的维度;use是对缺失值的处理方式;method给出计算相关系数所使用的方法,即上面所探讨的pearson相关系数、spearman相关系数和kendall相关系数。
下面举例子来说明该函数的具体使用方法:
例1:假设对10户居民家庭的月可支配收入和消费支出进行调查,得到的原始资料如下:
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 消费支出 | 20 | 15 | 40 | 30 | 42 | 60 | 65 | 70 | 53 | 78 |
| 可支配收入 | 25 | 18 | 60 | 45 | 62 | 88 | 92 | 99 | 75 | 98 |
那么,居民的消费支出与可支配收入之间是否存在线性相关关系,计算出相关系数并分析。
在R语言中编写相关程序见下面:
x <- c(25,18,60,45,62,88,92,99,75,98) #定义向量x保存可支配收入
y <- c(20,15,40,30,42,60,65,70,53,78) #定义向量y保存消费支出
#绘制散点图,看看是否有线性关系
plot(x, y, xlab="可支配收入", ylab="消费支出", main="消费支出与可支配收入的散点图")
#这样从散点图可以看出大致是否成线性关系,是正相关还是负相关
#还可以在散点图中添加趋势线,观察大体趋势
abline(lm(y~x)) #添加趋势线,lm()是绘制y与x之间的线性方程
#正态性检验
#计算的W值越接近1,表明越接近正态性
shapiro.test(x) #检验x是否符合正态分布要求
shapiro.test(y) #检验y是否符合正态分布要求
cor(x,y) #计算相关系数,默认采用pearson相关系数
#可以使用method参数指定计算的系数类型
cor(x,y,method='pearson') #pearson法计算的相关系数
#相关性的显著性检验:原假设为变量间不相关
#使用cor.test()函数
cor.test(x,y) #默认使用pearson方法进行检验
cor.test(x,y,method="pearson") #可以指定使用pearson方法进行检验
绘制的散点图如下:
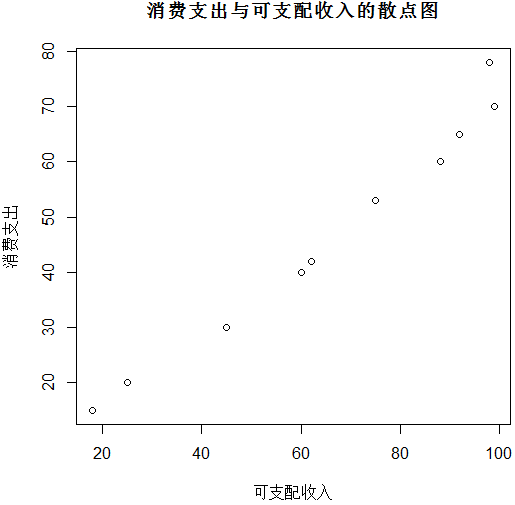
添加趋势线后的散点图:
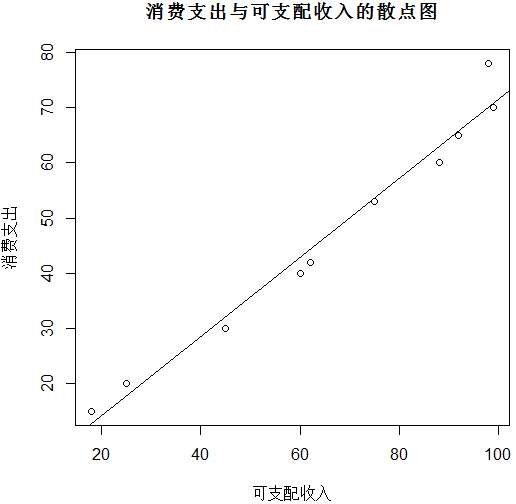
正态性检验的结果:

正态性原假设为总体服从正态分布,从检验结果来看,两变量的p-value均大于0.05,则在0.05的显著性水平下,不能拒绝原假设,即认为两个变量服从正态分布。
相关系数计算结果如下:
0.9877601
可以看出两个变量具有高度相关性,且相关系数大于0,则居民支出与销售收入具有高度的正相关性。
显著性检验结果:

从检验结果来看,p值<0.05,则在0.05的显著性水平下,相关系数较显著。
例2:检验智商和其每周花在 电视上的小时数的相关性,其数据如下:
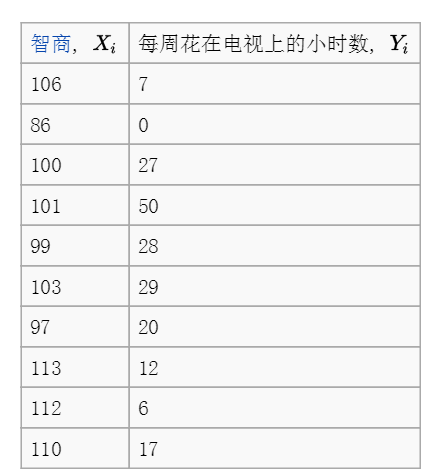
编写r程序如下:
#定义数据
x <- c(106,86,100,101,99,103,97,113,112,110)
y <- c(7,0,27,50,28,29,20,12,6,17)
#计算相关系数
cor(x,y,method="spearman")
#显著性检验
cor.test(x,y,method="spearman")
相关系数计算结果如下:
-0.1757576
检验结果如下图:

从检验结果来看,p值>0.05,则在0.05的显著性水平下,不能拒绝原假设,则相关系数不够显著。
上面的例子有些来源于网络。
新闻热点
疑难解答