使用R语言对两独立样本进行t检验

1、什么是两独立样本t检验

根据样本数据对两个样本来自的两个独立总体的均值是否有显著差异进行判断。

2、使用的前提条件

（1）两个样本应该是相互独立的；

（2）样本来自的两个总体应该服从正态分布。

3、问题描述

设总体x1服从正态分布N(μ₁，σ₁²)，总体x2服从正态分布N(μ₂,σ₂²)，分别从两个总体中抽取两组样本：(X₁₁,x₁₂,...,x_1m)和(x₂₁,x₂₂,...,x_2n),且两个样本相互独立。则检验μ₁和μ₂是否有显著性差异。

检验方法：

（1）提出假设

H0：μ1 = μ2

H1：μ1 ≠ μ2

（2）建立检验统计量

一般分两种情况，方差齐而未知；另外一种情况两总体方差不齐而未知。这两种情况计算统计量t的方法不同。所以在实际中应判断一下两独立总体的样本方差是否相等，并选择不同的方法来判断。

（3）计算检验统计量的观测值和p值

（4）在给定的显著性水平上做出判断决策

4、R语言中进行两个独立样本t检验的方法

在R语言中使用t.test()函数可以实现对两个独立样本的t检验。

t.test()函数的使用形式可以参见本站中的文章《使用R语言进行单样本t检验》中关于t.test()函数的介绍。

5、R语言中进行两个独立样本t检验举例

（1）使用甲乙两台机床来加工同种零件，两种机床加工零件的尺寸服从正态分布，且方差相同，为检验甲乙两台机床加工的零件尺寸均值是否一致（α=0.05），从两种机床加工的零件中分别抽取若干零件测得的其尺寸如下：

甲：20.5,19.8,19.7,20.4,20.1,20.0,19.0,19.9

乙：20.7,19.8,19.5,20.8,20.4,19.6,20.2

在R中编写程序如下：

#甲机床加工数据
x1<-c(20.5,19.8,19.7,20.4,20.1,20.0,19.0,19.9)
#乙机床加工数据
x2<-c(20.7,19.8,19.5,20.8,20.4,19.6,20.2)
#进行两样本t检验，指定方差相等
t.test(x1,x2,var.equal=T)

 计算结果如下图所示：

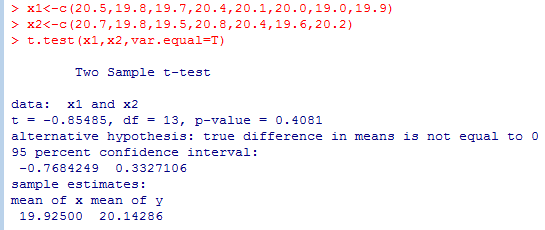
 从计算结果来看，t=-0.85485，p-value=0.4081，由于计算的p值>0.05，则不能拒绝原假设，即认为两台机床加工零件的尺寸均值没有显著性区别，也即认为均值相同。同时结果也给出了两台机床加工零件尺寸样本数据的均值分别为：19.925和20.14286。

由于题目中给出了两台机床的方差相同，所以这里在使用t.test()函数进行检验时，指定了参数var.equal=T.

（2）为了检验两种供热设备的能耗是否相同。测量两种设备（电动气闸和热活化气闸）的能耗数据如下 。您要确定是否有证据证明这两种设备之间的差值不为零，以比较出这两种设备的功效。
数据如下:

热活化气闸数据：

13.07,7.6,3.2,9.28,9.73,11.73,9.67,10.76,11.05,17.63,15.58,12.53,11.87,14.19,6.84,11.89,7.41,7.42,
10.83,9.44,12.94,13.15,11.69,7.73,11.94,13.62,17.07,14.66,9.56,12.37,8.33,8.67,11.27,11.67,9.37,8.93,
8.41,12.85,5.27,10.02,7.87,11.82,14.42,13.69,10.77,15.26,14.53,6.84,10.92,13.05

电动气闸数据：

8.25,9.66,8.33,8.82,12.06,9.67,17.51,10.79,13.59,7.99,12.64,14.42,9.25,7.79,
11.29,10.26,9.46,14.77,7.21,4.29,9.81,8.41,6.78,16.3,9.01,11.41,12.37,13.28,7.24,
10.55,13.89,10.72,9.22,10.61,10.04,10.2,20.55,11.75,7.08,5.5

在R中编写程序如下：

#热活化气闸数据
x1<-c(13.07,7.6,3.2,9.28,9.73,11.73,9.67,10.76,11.05,17.63,15.58,12.53,11.87,
14.19,6.84,11.89,7.41,7.42,10.83,9.44,12.94,13.15,11.69,7.73,11.94,13.62,17.07,
14.66,9.56,12.37,8.33,8.67,11.27,11.67,9.37,8.93,8.41,12.85,5.27,10.02,7.87,
11.82,14.42,13.69,10.77,15.26,14.53,6.84,10.92,13.05)
#电动气闸数据
x2<-c(8.25,9.66,8.33,8.82,12.06,9.67,17.51,10.79,13.59,7.99,12.64,14.42,9.25,
7.79,11.29,10.26,9.46,14.77,7.21,4.29,9.81,8.41,6.78,16.3,9.01,11.41,12.37,
13.28,7.24,10.55,13.89,10.72,9.22,10.61,10.04,10.2,20.55,11.75,7.08,5.5)

#若方差相等
t.test(x1,x2,var.equal=T,conf.level=0.95)

#若假定方差不等
t.test(x1,x2,var.equal=F)

假定方差相等时的运行结果如下：

假定方差不等时的运行结果如下：

从上面两个运行结果来看，p值都大于0.05，则可以认为两种供暖设备的能耗在统计上没有显著区别。

在实际中可以使用R语言提供的相关函数（如var.test()）对两组数据的方差齐次性进行检验，以便选择使用不同的方法进行检验。