1、方差分析的基本概念
方差分析(Analysis of Variance, ANOVA),由英国统计学家费雪(Ronald Aylmer Fisher)于1920年前后提出,最初主要应用于生物和农业田间试验,后来推广到各个领域。
它直接对多个总体的均值是否相等进行检验。
方差分析能够解决多个均值是否相等的检验问题。
方差分析是要检验各个水平的均值是否相等,采用的方法是比较各水平的方差。
如研究不同的销售点(假设为5个)对销售量是否有有影响,可以收集不同销售点若干天的销售数据来进行研究,则实质上是看这些销售点在这些天中的平均销售量 是否相同(或由显著差异)。
所要检验的对象称为因素或因子,也称为自变量。如例子中的销售点就是因素。
因素的不同表现称为水平或处理 。如例子中研究的是5个销售点,则共有5个水平。
每个因素水平下得到的样本数值称为观测值 ,也称为因变量或响应变量。
如果研究中只考虑一个因素的话,称之为单因素方差分析;如果考虑两个因素的话,称为双因素方差分析;双因素方差分析中如果不考虑两个因素的交互作用对因变量的影响的话,称之为无交互作用的双因素方差分析,否则称之为有交互作用的双因素方差分析。
2、方差分析的原假设与备择假设
原假设:
H0: μ1= μ2 = μ3 = μ4 = ...... = μn
备择假设:
H1:均值不全相等。
3、方差分析运用的前提条件
(1)各样本是相互独立的随机样本——独立性;
(2)各组的方差相同——方差齐性;
(3)各样本来自正态分布——正态性。
4、单因素方差分析问题原型
研究仅涉及到一个因素。如例子中的研究仅考虑销售点一个因素。
(1)问题原型
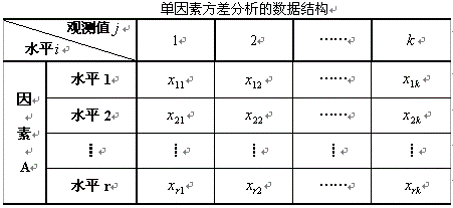
设因素A有r个水平A1,A2,...,Ar,每个水平Ai进行ni次独立观测,将水平Ai下的试验结果xi1,xi2,...,xini看成来自第i个正态总体Xi~N(μi,σ)的样本观测值,其中μi,σ均未知,并且每个总体Xi都相互独立。考虑线性统计模型:
xij = u i + εij
εij~N(0,σ2) 且相互独立
其中,μi为第i个总体的均值,ε为相应的试验误差。
(2)单因素方差分析的数据结构
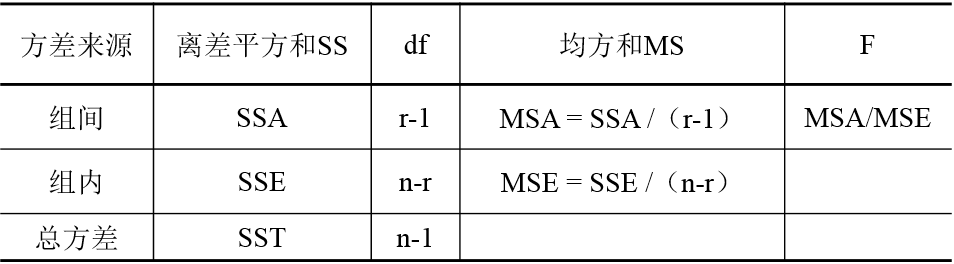
(3)单因素方差分析表
(4)判断与结论
在假设条件成立时,F统计量服从第一自由度为r-1、第二自由度为n-r的 F分布。
若F ≥ Fα,则拒绝原假设,表明均值之间的差异显著,因素A对观察值有显著影响;
若F < Fα,则不能拒绝原假设,表明均值之间的差异不显著,因素A对观察值没有显著影响。
5、R中进行方差分析的函数
在R中可以使用aov()函数和summary()函数共同完成方差分析的计算。aov()函数的格式如下:
aov(formula, data = NULL, projections = FALSE, qr = TRUE, contrasts = NULL, ...)
其中,formula是个字符串,表示方差分析的公式,如形如X~A或X~A+B或X~X+B+A:B;
data是数据框,描述数据的响应变量、因素和相应水平的对应关系,默认值为NULL,当数据直接由X和A给出时,不需要此参数。
6、R语言进行单因素方差分析举例说明
新实验楼装修,小明需要买一批灯泡。市场上的灯泡种类繁多,而且价格也相差较大。小明选择了4种品牌的灯泡请人做了测试。测试结果如下表。你认为购买哪种品牌较好呢?
| 品牌 | 使用寿命 | |||||||
| A1 | 1600 | 1610 | 1650 | 1680 | 1700 | 1700 | 1780 | |
| A2 | 1500 | 1640 | 1400 | 1700 | 1750 | |||
| A3 | 1640 | 1550 | 1600 | 1620 | 1640 | 1600 | 1740 | 1800 |
| A4 | 1510 | 1520 | 1530 | 1570 | 1640 | 1600 | ||
当然选择平均寿命要大一些的,那么这些水平均值有区别吗?如何进行分析:方差分析。
在R中编写程序如下:
#单因素方法分析
#定义数据灯泡寿命向量
X<-c(1600,1610,1650,1680,1700,1700,1780,
1500,1640,1400,1700,1750,
1640,1550,1600,1620,1640,1600,1740,1800,
1510,1520,1530,1570,1640,1600)
#定义一个因子用于指定每个数据所属的组
A<-factor(rep(1:4,c(7,5,8,6))) #使用重复函数进行定义
#定义数据框
lamp<-data.frame(X,A)
#进行方差分析
lampAov<-aov(X~A,projections=F)
#提取方差分析表
sm<-summary(lampAov)
print(sm) #输出方差分析信息
#数据满足正态性要求吗?
#对数据进行正态性符合性检验(Shapiro-Wilk)
#该检验中计算的W值越接近1,正态性越好
#对数据框中的X列值因素水平为1的进行正态性检验
shapiro.test(lamp$X[lamp$A==1])
#对数据框中的X列值因素水平为2的进行正态性检验
shapiro.test(lamp$X[lamp$A==2])
#对数据框中的X列值因素水平为3的进行正态性检验
shapiro.test(lamp$X[lamp$A==3])
#对数据框中的X列值因素水平为4的进行正态性检验
shapiro.test(lamp$X[lamp$A==4])
#当水平数较多时,运用上面的写法比较麻烦,可以借助with()函数和tapply()函数
with(lamp,tapply(X,A,shapiro.test))
#方差齐性检验
bartlett.test(X~A,data=lamp)
在R中的运行结果如下:

从结果中看,P值>0.05,则在0.05的显著性水平下,没有充分理由拒绝原假设,也就是说4种品牌的寿命没有显著性区别,则在购买时,挑拣便宜的进行购买就行了。
正态性检验结果如下:

从检验结果来看,各组数据都符合正态性。
方差齐性检验结果:

由检验结果的p值=0.1215 > 0.05可知,在0.05的置信水平下,没有充分理由拒绝原假设(每组的方差相等),则可以认为每组的方差相等,即满足方差齐性。
新闻热点
疑难解答