R语言中矩阵的使用

2023-05-01 13:45:48

字体：大中小

来源：转载

供稿：网友

在R语言中，矩阵（matrix）是将数据按行和列组织数据的一种数据对象，相当于二维数组，可以用于描述二维的数据。与向量相似，矩阵的每个元素都拥有相同的数据类型。通常用列来表示来自不同变量的数据，用行来表示相同的数据。

1、R语言中矩阵的创建

在R语言中可以使用matrix()函数来创建矩阵，其语法格式如下：

matrix(data=NA, nrow = 1, ncol = 1, byrow = FALSE, dimnames = NULL)

参数含义如下：

data：矩阵的元素，默认为NA，即未给出元素值的话，各项为NA

nrow：矩阵的行数，默认为1；

ncol：矩阵的列数，默认为1；

byrow：元素是否按行填充，默认按列；

dimnames：以字符型向量表示的行名及列名。

（1）创建形式1

m1 <- matrix(c(1:6),nrow=2,ncol=3,dimnames=list(c("r1","r2"),c("c1","c2","c3")))

（2）创建形式2

m2 <- matrix(1:6,nrow=2) #共6个元素，分2行，每行3个元素，未指定行名和列名

（3）创建形式3

m3 <- matrix(1:6,ncol=3) #共6个元素，结果与创建形式2相同

（4）创建形式4

m4 <- matrix(nr=2,nc=3) #未指定元素数据，默认为NA，2行3列，nr是nrow的简写，nc是ncol的简写，R能识别

以上4中形式的执行效果如下图所示：

R语言中创建矩阵的方法

（5）创建形式5

使用rbind函数或cbind函数可以将两个向量或矩阵合并为一个矩阵

v1 <- c(1:4) #创建名为v1的向量

v2 <- c(5:8) #创建名为v2的向量

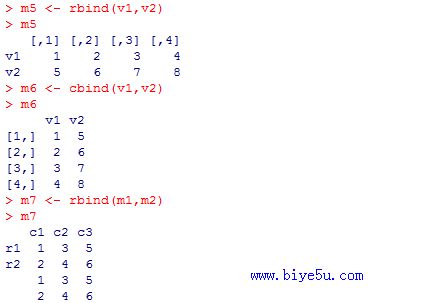
m5 <- rbind(v1,v2) #将向量v1和v2按行合并为一个矩阵

m6 <- cbind(v1,v2) #将向量v1和v2按列合并为一个矩阵

m7 <- rbind(m1,m2) #将上面定义的矩阵m1和m2合并为一个新的矩阵

本部分的执行效果见下图

R语言中使用rbind函数和cbind函数生成新矩阵

2、R语言中矩阵的索引

R语言中，矩阵的索引方式主要有以下几种：

直接使用矩阵名可以获得整个矩阵的情况，如下图：

R语言中使用矩阵名输出矩阵所有元素

（1）矩阵名[行位置,列位置] 获取某个元素的值

m1[2,1] #输出矩阵m1第2行第1列的元素值：2

（2）矩阵名[行位置, ] 获取某一行的所有元素

m1[2, ] #输出矩阵m1中第2行的数据

（3）矩阵名[ , 列位置] 获取某一列的所有元素

m1[ ,2] #输出矩阵m1中第2列的所有元素

（4）矩阵名[ "行名"，"列名"] 通过行名和列名获取某一个元素

m1["r1", "c2"]

（5）矩阵名["行名", ] 通过行名来获取矩阵某一行的所有元素

m1["r2", ]

（6）矩阵名[ , "列名"] 通过列名来获取矩阵某一列的所有元素

m1[ , "c1"]

（7）矩阵名[ -r, -c] 排除第r行和第c列数据

m1[-1, -2] #除去第1行及第2列的数据

以上部分的执行结果见下图：

R语言中矩阵的主要索引方式

（8）矩阵名[-r , ] 除去第r行之外的数据

m1[-2,] #除去第2行之外的数据

（9）矩阵名[ , -c] 除去第c列之外的数据

m1[, -2] #除去第2列之外的数据

以上两种情况的执行结果：

R语言中矩阵排除指定的元素或行货列的方法

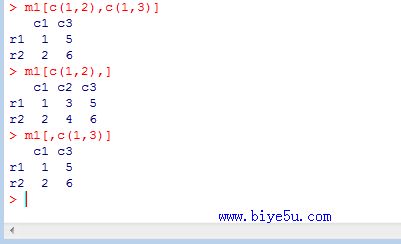
（10）矩阵名[向量1，向量2] 获取向量1表示的行集和向量2表示的列集交叉处的数据

m1[c(1,2),c(1,3)]

（11）矩阵名[向量1, ]获取向量1表示的行集的数据

m1[c(1,2), ]

（12）矩阵名[, 向量2] 获取向量2表示的列集的数据

m1[ , c(1,3)]

以上三种情况的执行结果：

R语言中使用向量访问矩阵的元素

（13）矩阵名[-向量1, -向量2] 获取除指定行集和列集之外的元素

m1[-c(1),-c(2,3)]

（14）矩阵名[-向量1, ]获取除指定行集之外的元素

m1[-c(2), ]

（15）矩阵名[ , -向量2] 获取除指定列集之外的元素

m1[ , -c(1:2)]

（16）矩阵名[行名称向量，列名称向量] 获取指定行名称和列名称的元素，或只指定行名称向量，或列向量均可

m1[c("r1","r2"), c("c1","c3")]

m1[c("r1,"r2") , ]

m1[ , c("c1","c3")]

注意在以上使用矩阵的索引或向量表示的索引集时，索引不能超过矩阵的最大维数。

3、矩阵的编辑

（1）修改矩阵元素的值

在R语言中，主要通过以下几种形式来修改矩阵中的元素值。

①修改单个值

m1[1,2] = 12 #将矩阵m1中第1行第2个元素的值修改为12

m1["r2","c2"] = 22 #将矩阵m1中行名称为r2与列名称c2交叉处的元素值修改为22

②修改某一行的数据

m1[2,] = c(21,22,23) #将矩阵第2行的数据修改为21,22,23

m1["r1" ,] = c(11:13) #将矩阵名称为r1的行的数据修改为11 ，12, 13

m1[1, ] = 0 #将矩阵m1的第一行的数据都修改为0

③修改某一列的数据

m1[, 1] = c(11,21) #将矩阵的第一列数据修改为11,21

m1[, "c2"] = c(221,222) #将矩阵中名为c2的列数据改为221,222

m1[,3 ] = 333 #将矩阵第3列的数据都修改为333

注意下面这种情况：

ma <- (1:16, nr=4) #创建名为ma的矩阵，共4行4列

输出

[,1] [,2] [,3] [,4]

[1,] 1 5 9 13

[2,] 2 6 10 14

[3,] 3 7 11 15

[4,] 4 8 12 16

修改第2列的数据：

ma[,2] = c(12,22) #这样，向量的数据可以重复以补齐到与矩阵ma的行数相同

即第2列的数据变为 12 22 12 22

但是如果向量中提供的元素个数不能被替换对象的维数整除的话，会报错，也就是说这里要替换的列元素有4个，提供了2个，2能被4整除，则其通过重复循环向量2次可以将矩阵列元素补齐，但如提供的向量元素有3个的话，会给出“被替换的项目不是替换值长度的倍数”的错误。即对于ma矩阵，其行或列给出替换的元素个数只能是1或2或4，其余会报错。

（2）删除指定的行或列

m1 <- m1[-2,] #删除第2行

m1 <- m1[,-2] #删除第2列

m2<- m2[-1,-2] #删除矩阵的第1行以及第2列

注意，上面使用了给矩阵重新赋值的方式，否则不能实现删除操作，仅是访问。

（3）矩阵的合并

可以使用上面所说的rbind和cbind函数进行合并

m1<-rbind(m1,c(31,32,33)) #将向量按行合并到矩阵m1中

m1<-cbind(m1,c(44,45)) #将向量按列合并到矩阵m1中

同样，上面给出的向量元素不足时，循环使用，同样当元素个数不足时，其提供的元素个数应能被对应的行维或列维除尽，即列数或行数需是所提供的元素个数的整数倍。

4、矩阵的常用运算

（1）colSums(m1) 求矩阵各列的和