在数据库的关系代数中,专门的关系运算包括选择,投影,连接和除。本文主要探讨一下连接运算。
连接运算是二元关系操作,以符号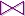 表示连接,它的定义为:
表示连接,它的定义为:
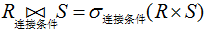
连接与笛卡尔积的区别在于笛卡尔积包含两个关系的所有元组的组合,而连接只包含那些满足连接条件的元组的组合。如果没有连接条件,即无条件连接,则连接变成笛卡尔积。因此,在关系数据模型中连接可用笛卡尔积表示。笛卡尔积可以看成连接的特例。连接条件为两关系中对应属性的比较,所谓对应属性不一定同名,但要有相同的域。其普遍形式可表示为:
<条件1> and <条件2> and … and <条件k>
其中,每个条件的普遍形式为:
AiθBj
Ai为R的一个属性,Bj为S中与Ai对应的属性,θ∈{=,<,≤,>,≥,≠}。这种普遍的连接又称为θ连接。在有些DBMS中,允许连接条件为对应属性的函数的比较,对应属性的域不一定相同,但两个函数的域要一样。如果所有条件中的θ都为=,则此种连接称为等值连接。在等值连接的结果中,对应属性的值是相同的,没有必要重复列出,只要在两个对应属性中取一个就可以了。这种消除冗余属性的等值连接称为自然连接。自然连接在关系模型中用得很多,关系间的联系主要靠自然连接来实现。自然连接一般记为R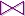 S。它等于如下的操作:
S。它等于如下的操作:
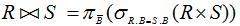
即若R和S具有相同的属性组B,则自然连接是选择R与S笛卡尔积中B属性值相同的元组,同时并去除重复的属性B(式中用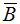 表示)。
表示)。
设关系R和S分别由表1、表2给出,请求出下列的关系操作结果:
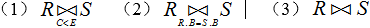

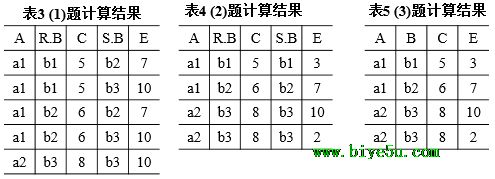
根据上面的讲解,求得的各操作结果如表3、表4和表5所示。
新闻热点
疑难解答