在R语言中实现排列与组合

所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。（摘自百度百科）

一、定义与公式

1、排列的定义及公式

从n个不同元素中，任取r（m≤r，r与n均为自然数，下同）个元素按照一定的顺序排成一列，叫做从n个不同元素中取出r个元素的一个排列；从n个不同元素中取出r(r≤n）个元素的所有排列的个数，叫做从n个不同元素中取出r个元素的排列数，用符号 p(n,r)表示。

其公式为：

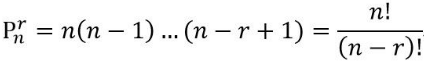
2、组合的定义及公式

从n个不同元素中，任取r(r≤n）个元素并成一组，叫做从n个不同元素中取出r个元素的一个组合；从n个不同元素中取出r(r≤n）个元素的所有组合的个数，叫做从n个不同元素中取出r个元素的组合数。用符号 C(n,r) 表示。

计算公式为：

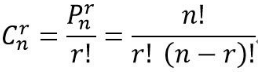
同时，C^r_n = C^n-r_n

二、R中的相关函数

在R中可以使用prod函数计算排列问题，使用choose函数计算组合问题。

1、prod函数

prod函数计算数字的连乘积。其格式如下：

prod(..., na.rm = FALSE)

其中，...是参与计算的数字（复数、逻辑）向量；na.rm表示是否忽略缺失值（NA），默认为FALSE。

注意：当na.rm为FALSE时，参与计算的向量中若有NA值，则返回NA，否则会忽略向量中的NA值。

下面举个例子说明该函数的使用：

> prod(1:8)
 [1] 40320

上面这个例子相当于计算8的阶乘：8! = 40320

> prod(3:5)
 [1] 60

上面这个例子相当于计算：3 × 4 × 5 = 60

2、choose函数

choose函数的形式如下：

choose(n, k)

用于计算下列情形的问题：

n(n-1)…(n-k+1) / k! = n! / [(n-k)! k!] = C(n,k)

三、R中排列组合计算例子

1、从1~5五个数字中，任意抽取2个不同的数字，一共有多少种数字组合方法。

这是组合问题，没有顺序问题，则C(5, 2) = 5!/(3!×2!) = 10，即有10中组合情况。

在R中计算如下：

> choose(5, 2)
 [1]  10

在R中可以使用combn函数列出所有的组合情况，如本例中，可以使用下面的代码，查看组合情况：

> combn(5, 2)
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,]    1   1  1   1  2  2   2   3  3   4
[2,]    2   3  4   5  3  4   5   4  5   5
 

2、从1~5五个数字中，任意抽取2个不同的数字，如果考虑两个数字抽取的先后顺序，则有多少种情况。

因为这里考虑了抽取数字的先后顺序，是排列问题，则A(5,2) = 5! / (5-2)! = 20，即有20种组合顺序。

可能的组合为：

(1,2),(1,3),(1,4),(1,5),
(2,1),(2,3),(2,4),(2,5),
(3,1),(3,2),(3,4),(3,5),
(4,1),(4,2),(4,3),(4,5),
(5,1),(5,2),(5,3),(5,4)

在R中计算如下：

> prod(1:5) / prod(1:3)
  [1] 20

或者使用下面的R语句：

> choose(5,2) * prod(1:2)
  [1] 20

也可以使用下面的R语句：

> choose(5,2) * factorial(2)
 [1] 20

后面两种情况，利用了排列和组合公式之间的关系进行推导而来的。

在第3个R代码中使用了factorial()函数，该函数的作用计算某个数值的阶乘，其原型如下：

factorial(x),这里当x的值为0时，则返回1.其余返回x(x-1)....1的连乘积，相当于prod(1:x)