R中求解一元方程的方法

在R中可以使用uniroot函数来求解一元方程。

R中uniroot函数的语法形式如下：

uniroot(f, interval, ..., 
lower = min(interval), upper = max(interval),
f.lower = f(lower, ...), f.upper = f(upper, ...), 
extendInt = c("no", "yes", "downX", "upX"), check.conv = FALSE, 
tol = .Machine$double.eps^0.25, maxiter = 1000, trace = 0)

主要参数的含义如下：

（1）f 要求解的方程；

（2）interval 用向量表示的区间；

（3）lower,upper 用于搜索解的下限和上限；

（4）tol 求解的精度；

（5）maxiter 最大迭代次数

该函数的结果是一个列表，包括4个部分：求解的根root和在该点的函数值f.root；迭代次数iter和求解方程的近似估计的精度estim.prec。

下面举几个例子来说明一下具体使用方法：

（1）求解一元一次方程

求解形如ax+b=0的根。如求解 3x + 2 = 0的根：

f <- function(x, a, b) { return (a * x + b) }
root <- uniroot(f, c(-5, 0), a = 3, b = 2,  tol=0.0001)
root$root  #输出根
root$f.root #输出x值为求解的根时的函数值

以上运行结果如下图所示：

上面的程序也可以写成下面的形式：

root<-uniroot(function(x,a,b) a*x+b,a=3,b=2,lower=-5,upper=0,tol=0.0001)

结果是一样的。

（2）求解一元二次方程

求解形如f(x)=ax² + bx + c的方程的解。如求出方程x² - x - 6 = 0的根。

f <- function(x, a, b, c) { return (a * x ^ 2 + b * x + c)}
re<-uniroot(f,c(-3,0),a=1,b=-1,c=-6,tol=1e-9)
re$root #输出根
re$f.root #当方程取值根时的方程结果
re$iter  #求解的迭代次数

运算结果如下图所示：

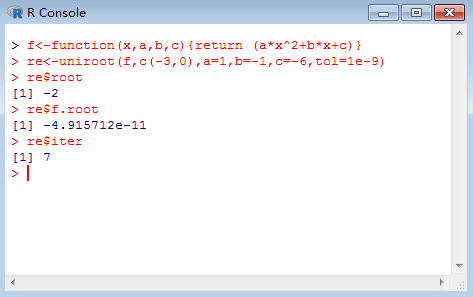
 从上图可以看出该方程的一个根为-2，改变它的运算区间可以求出另外一个根：

re<-uniroot(f,c(0,3),a=1,b=-1,c=-6,tol=1e-9)
re$root

这里求得的另外一个根为3.

由于uniroot()函数每次只能计算一个根，而且要求输入的区间端点值必须是正负号相反的。如果我们直接输入（-3, 4）这个区间，那么uniroot()函数会出现错误：

Error in uniroot(f, c(-3, 4), a = 1, b = -1, c = -6, tol = 1e-09) : 
位于极点边的f()值之正负号不相反

即要求f(lower) * f(upper) <=0。

那么在实际中如何确定根的大致范围呢，一个做法就是通过绘图来观察，如本例中可以使用西面的代码来绘图：

f<-function(x,a,b,c){return (a*x^2+b*x+c)}
X<-seq(-6,6,by=0.1)
Y<-f(X,a=1,b=-1,c=-6)
plot(X,Y,type="l",col=2)  #绘制函数图形
abline(h=0,v=0,lty=2,col="gray")   #绘制出横轴和纵轴

绘图结果如下图所示：

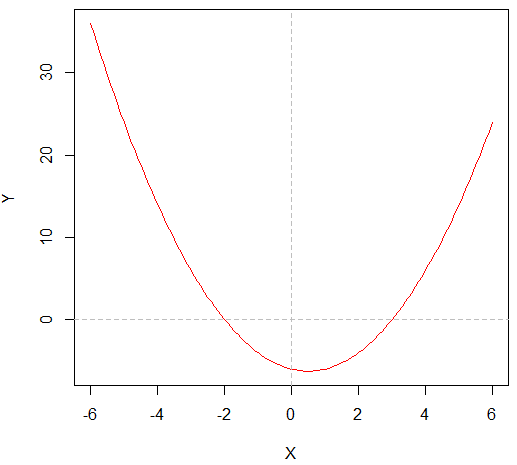
从图中可以看出，方程的一个根位于-3和0之间，另外一个根位于2和4之间，这样我们取区间（-3,0）和（0,4）即可。同时也可以看出这两个区间的两个端点的函数值得符号是相反的。

（3）求解一元三次方程

求解形如ax³+bx²+cx+d=0的根。如求x³-x-3=0的方程根。

程序如下：

f<-function(x,a,b,c,d) {return(a*x^3+b*x^2+c*x+d)}
a<-1
b<-0
c<- -1
d<- -3
X<-seq(-3,4,by=0.01)
Y<-f(X,a=a,b=b,c=c,d=d)
plot(X,Y,type="l",col=3)
abline(h=0,v=0,col="gray")
re<-uniroot(f,c(1,2.5),a=a,b=b,c=c,d=d,tol=1e-10)
re$root
re$f.root
re$iter

求解结果如下：

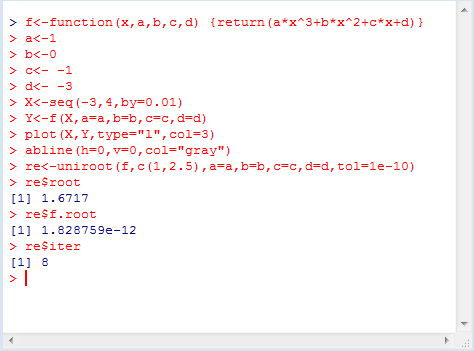
绘制的曲线如下图所示：

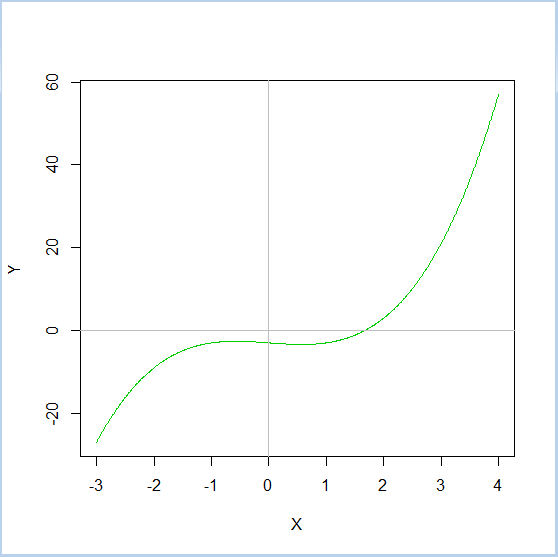
从图中可以看出方程的根在区间（1,3）之间，且求得的根为1.6717