python实现梯度下降算法

梯度下降（Gradient Descent）算法是机器学习中使用非常广泛的优化算法。当前流行的机器学习库或者深度学习库都会包括梯度下降算法的不同变种实现。

本文主要以线性回归算法损失函数求极小值来说明如何使用梯度下降算法并给出python实现。若有不正确的地方，希望读者能指出。 

梯度下降

梯度下降原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快。

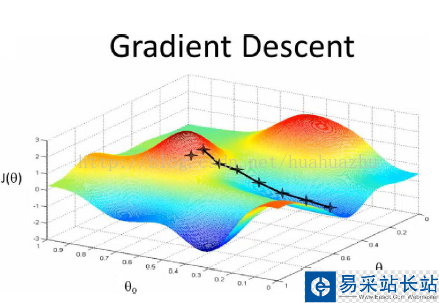
在线性回归算法中，损失函数为

在求极小值时，在数据量很小的时候，可以使用矩阵求逆的方式求最优的θ值。但当数据量和特征值非常大，例如几万甚至上亿时，使用矩阵求逆根本就不现实。而梯度下降法就是很好的一个选择了。

使用梯度下降算法的步骤：

1）对θ赋初始值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得目标损失函数J(θ)按梯度下降的方向进行减少。

其中为学习率或步长，需要人为指定，若过大会导致震荡即不收敛，若过小收敛速度会很慢。

3）当下降的高度小于某个定义的值，则停止下降。

另外，对上面线性回归算法损失函数求梯度，结果如下：

在实际应用的过程中，梯度下降算法有三类，它们不同之处在于每次学习(更新模型参数)使用的样本个数，每次更新使用不同的样本会导致每次学习的准确性和学习时间不同。下面将分别介绍原理及python实现。

 批量梯度下降(Batch gradient descent)   

每次使用全量的训练集样本来更新模型参数，即给定一个步长，然后对所有的样本的梯度的和进行迭代： 

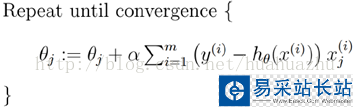
梯度下降算法最终得到的是局部极小值。而线性回归的损失函数为凸函数，有且只有一个局部最小，则这个局部最小一定是全局最小。所以线性回归中使用批量梯度下降算法，一定可以找到一个全局最优解。

优点：全局最优解；易于并行实现；总体迭代次数不多
缺点：当样本数目很多时，训练过程会很慢，每次迭代需要耗费大量的时间。

随机梯度下降(Stochastic gradient descent) 

随机梯度下降算法每次从训练集中随机选择一个样本来进行迭代，即：