使用遗传算法求二元函数的最小值

二元函数为y=x1^2+x2^2,x∈[-5,5]

NIND=121;  %初始种群的个数(Number of individuals)NVAR=2;   %一个染色体（个体）有多少基因PRECI=20;  %变量的二进制位数(Precision of variables)MAXGEN=200;  %最大遗传代数(Maximum number of generations)GGAP=0.8;  %代沟(Generation gap)，以一定概率选择父代遗传到下一代trace=zeros(MAXGEN,2);   %寻优结果的初始值Chrom=crtbp(NIND,PRECI*NVAR); %初始种群%区域描述器(Build field descriptor)%确定每个变量的二进制位数，取值范围，及取值范围是否包括边界等。FieldD=[rep([PRECI],[1,NVAR]);rep([-5;5]，[1,NVAR]);rep([1;0;1;1],[1,NVAR])];Objv=objfun(bs2rv(Chrom,FieldD))gen=1;     %代计数器while gen<=MAXGEN Fitv=ranking(Objv); %分配适应度值(Assign fitness values) SelCh=select('sus',Chrom,Fitv,GGAP); %选择 SelCh=recombin('xovsp',SelCh,1);  %重组 SelCh=mut(SelCh);      %变异 ObjVSel=objfun(bs2rv(SelCh,FieldD));%子代个体的十进制转换 %重插入子代的新种群 [Chrom,Objv]=reins(Chrom,SelCh,1,1,Objv,ObjVSel); trace(gen,1)=min(Objv);   %遗传算法性能跟踪 trace(gen,2)=sum(Objv)/length(Objv);  gen=gen+1;     %代计数器增加endplot(trace(:,1));hold onplot(trace(:,2),'.')gridlegend('最优解的变化','解的平均值的变化')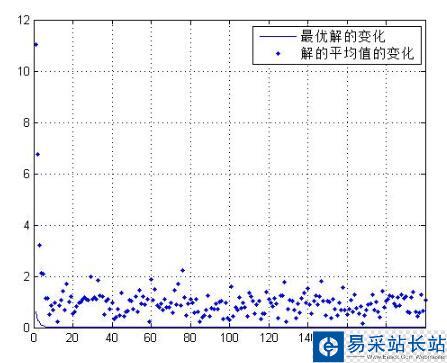

根据上面的求解模型，可以写出模型的.M文件如下，即适应度函数

% OBJFUN.M  % Syntax: ObjVal = objfun1(Chrom,rtn_type)%% Input parameters:% Chrom  - Matrix containing the chromosomes of the current%    population. Each row corresponds to one individual's%    string representation.%    if Chrom == [], then special values will be returned% rtn_type - if Chrom == [] and%    rtn_type == 1 (or []) return boundaries%    rtn_type == 2 return title%    rtn_type == 3 return value of global minimum%% Output parameters:% ObjVal - Column vector containing the objective values of the%    individuals in the current population.%    if called with Chrom == [], then ObjVal contains%    rtn_type == 1, matrix with the boundaries of the function%    rtn_type == 2, text for the title of the graphic output%    rtn_type == 3, value of global minimum% Author:  YQ_youngerfunction ObjVal = objfun(Chrom,rtn_type);% Dimension of objective function Dim = 2; % Compute population parameters [Nind,Nvar] = size(Chrom);% Check size of Chrom and do the appropriate thing % if Chrom is [], then define size of boundary-matrix and values if Nind == 0  % return text of title for graphic output  if rtn_type == 2   ObjVal = ['DE JONG function 1-' int2str(Dim)];  % return value of global minimum  elseif rtn_type == 3   ObjVal = 0;  % define size of boundary-matrix and values  else    % lower and upper bound, identical for all n variables     ObjVal = 1*[-5; 5];   ObjVal = ObjVal(1:2,ones(Dim,1));  end % if Dim variables, compute values of function elseif Nvar == Dim  % function 1, sum of xi^2 for i = 1:Dim (Dim=30)  % n = Dim, -5 <= xi <= 5  % global minimum at (xi)=(0) ; fmin=0  ObjVal = sum((Chrom .* Chrom)')';  % ObjVal = diag(Chrom * Chrom'); % both lines produce the same % otherwise error, wrong format of Chrom else  error('size of matrix Chrom is not correct for function evaluation'); end % End of function