因为是可逆的,所以像那种md5,sha之类的不可逆加密就没法用了,然后可逆的加密主要是分为对称加密盒非对称加密:
对称加密:用加密的钥匙来解密,比如DES,AES的加解密
非对称加密:一个钥匙加密,用另一个钥匙解密,这个主要就是RSA比较成熟(点我看科普)
当然这么看来非对称加密更加适合我这个需求,然后我又各种找RSA,.NET中自己实现了加密RSA加密类RSACryptoServicePRovider,但是这个用起来着实不爽,公钥和私钥是用xml来显示,太长太大,而且由于没有实现一些标准,只能用公钥加密,私钥解密(这个XML种私钥中可以看出公钥),但是事实上RSA的一对有效密钥公钥加密私钥解密 和私钥加密公钥解密均可 我想要的是后面的效果啊,结果又继续各种找,在找了好久看不到希望之际时,在csdn和博客园上看到了这两篇文章:
C#使用RSA私钥加密公钥解密的改进,解决特定情况下解密后出现乱码的问题
这两个正好可以实现我的需求,但是上面的代码都不全,说的倒是很清楚了,就是说利用一个开源的大数组处理类Bigingegter类配合RSA的算法自己显示RSA的加解密,问题也解决的很到位了,单个文章中提供的资料都不好进行加解密,但是合起来就ok了,他们那个用的不爽,自己就在他们的基础上又封装了一个帮助类:
(我仅仅只是整合了他们的代码,方便自己用而已,嘿嘿,核心代码还是他们的)
按他们说的,先要产生密钥对,当然这个密钥对不是随便写的,是需要大质数 又素数啥啥啥的,不过RSACryptoServiceProvider这个类里面可以生成这些,还不错,先看下我生成的密钥对:

 View Code
View Code /// <summary> /// RSA加密的密匙结构 公钥和私匙 /// </summary> public struct RSAKey { public string PublicKey { get; set; } public string PrivateKey { get; set; } } #region 得到RSA的解谜的密匙对 /// <summary> /// 得到RSA的解谜的密匙对 /// </summary> /// <returns></returns> public static RSAKey GetRASKey() { RSACryptoServiceProvider.UseMachineKeyStore = true; //声明一个指定大小的RSA容器 RSACryptoServiceProvider rsaProvider = new RSACryptoServiceProvider(DWKEYSIZE); //取得RSA容易里的各种参数 RSAParameters p = rsaProvider.ExportParameters(true); return new RSAKey() { PublicKey = ComponentKey(p.Exponent,p.Modulus), PrivateKey = ComponentKey(p.D,p.Modulus) }; } #endregion#region 组合解析密匙 /// <summary> /// 组合成密匙字符串 /// </summary> /// <param name="b1"></param> /// <param name="b2"></param> /// <returns></returns> private static string ComponentKey(byte[] b1, byte[] b2) { List<byte> list = new List<byte>(); //在前端加上第一个数组的长度值 这样今后可以根据这个值分别取出来两个数组 list.Add((byte)b1.Length); list.AddRange(b1); list.AddRange(b2); byte[] b = list.ToArray<byte>(); return Convert.ToBase64String(b); } /// <summary> /// 解析密匙 /// </summary> /// <param name="key">密匙</param> /// <param name="b1">RSA的相应参数1</param> /// <param name="b2">RSA的相应参数2</param> private static void ResolveKey(string key, out byte[] b1, out byte[] b2) { //从base64字符串 解析成原来的字节数组 byte[] b = Convert.FromBase64String(key); //初始化参数的数组长度 b1=new byte[b[0]]; b2=new byte[b.Length-b[0]-1]; //将相应位置是值放进相应的数组 for (int n = 1, i = 0, j = 0; n < b.Length; n++) { if (n <= b[0]) { b1[i++] = b[n]; } else { b2[j++] = b[n]; } } } #endregion
主要是对生成的byte数组拼接成字符串(毕竟还是字符串给别人比较方便):因为公钥和私钥都是两个byte一起用才能加解密,所以将两个byte数组拼接成一个byte,把并添加一个标志位来使得后期可以解开,最后以base64字符串来传
有了自己封装的密钥之后
再封装类似AES,DES这种简单的入参进行加减密(不然传BitIngteger真心累)

 View Code
View Code #region 字符串加密解密 公开方法 /// <summary> /// 字符串加密 /// </summary> /// <param name="source">源字符串 明文</param> /// <param name="key">密匙</param> /// <returns>加密遇到错误将会返回原字符串</returns> public static string EncryptString(string source,string key) { string encryptString = string.Empty; byte[] d; byte[] n; try { if (!CheckSourceValidate(source)) { throw new Exception("source string too long"); } //解析这个密钥 ResolveKey(key, out d, out n); BigInteger biN = new BigInteger(n); BigInteger biD = new BigInteger(d); encryptString= EncryptString(source, biD, biN); } catch { encryptString = source; } return encryptString; } /// <summary> /// 字符串解密 /// </summary> /// <param name="encryptString">密文</param> /// <param name="key">密钥</param> /// <returns>遇到解密失败将会返回原字符串</returns> public static string DecryptString(string encryptString, string key) { string source = string.Empty; byte[] e; byte[] n; try { //解析这个密钥 ResolveKey(key, out e, out n); BigInteger biE = new BigInteger(e); BigInteger biN = new BigInteger(n); source = DecryptString(encryptString, biE, biN); } catch { source = encryptString; } return source; } #endregion #region 字符串加密解密 私有 实现加解密的实现方法 /// <summary> /// 用指定的密匙加密 /// </summary> /// <param name="source">明文</param> /// <param name="d">可以是RSACryptoServiceProvider生成的D</param> /// <param name="n">可以是RSACryptoServiceProvider生成的Modulus</param> /// <returns>返回密文</returns> private static string EncryptString(string source, BigInteger d, BigInteger n) { int len = source.Length; int len1 = 0; int blockLen = 0; if ((len % 128) == 0) len1 = len / 128; else len1 = len / 128 + 1; string block = ""; StringBuilder result = new StringBuilder(); for (int i = 0; i < len1; i++) { if (len >= 128) blockLen = 128; else blockLen = len; block = source.Substring(i * 128, blockLen); byte[] oText = System.Text.Encoding.Default.GetBytes(block); BigInteger biText = new BigInteger(oText); BigInteger biEnText = biText.modPow(d, n); string temp = biEnText.ToHexString(); result.Append(temp).Append("@"); len -= blockLen; } return result.ToString().TrimEnd('@'); } /// <summary> /// 用指定的密匙加密 /// </summary> /// <param name="source">密文</param> /// <param name="e">可以是RSACryptoServiceProvider生成的Exponent</param> /// <param name="n">可以是RSACryptoServiceProvider生成的Modulus</param> /// <returns>返回明文</returns> private static string DecryptString(string encryptString, BigInteger e, BigInteger n) { StringBuilder result = new StringBuilder(); string[] strarr1 = encryptString.Split(new char[] { '@' }, StringSplitOptions.RemoveEmptyEntries); for (int i = 0; i < strarr1.Length; i++) { string block = strarr1[i]; BigInteger biText = new BigInteger(block, 16); BigInteger biEnText = biText.modPow(e, n); string temp = System.Text.Encoding.Default.GetString(biEnText.getBytes()); result.Append(temp); } return result.ToString(); } #endregion
这样的话 用户用起来就很方便了 直接源码/加密码 +密钥就可以加解密了
使用方式如下

 View Code
View Code string str = "{/"sc/":/"his51/",/"no/":/"1/",/"na/":/"管理员/"}{/"sc/":/"@his51/",/"no/":/"1/",/"na/":/"管理员/"}{/"sc/":/"his51/",/"no/":/"1/",/"na/":/"管员/"}{/"sc/":/"his522"; RSAHelper.RSAKey keyPair = RSAHelper.GetRASKey(); Console.WriteLine("公钥:" + keyPair.PublicKey + "/r/n"); Console.WriteLine("私钥:" + keyPair.PrivateKey + "/r/n"); string en = RSAHelper.EncryptString(str, keyPair.PrivateKey); Console.WriteLine("加密后:"+en + "/r/n"); Console.WriteLine("解密:"+RSAHelper.DecryptString(en, keyPair.PublicKey) + "/r/n"); Console.ReadKey();
是不是简单又熟悉 ,下面来看一下效果
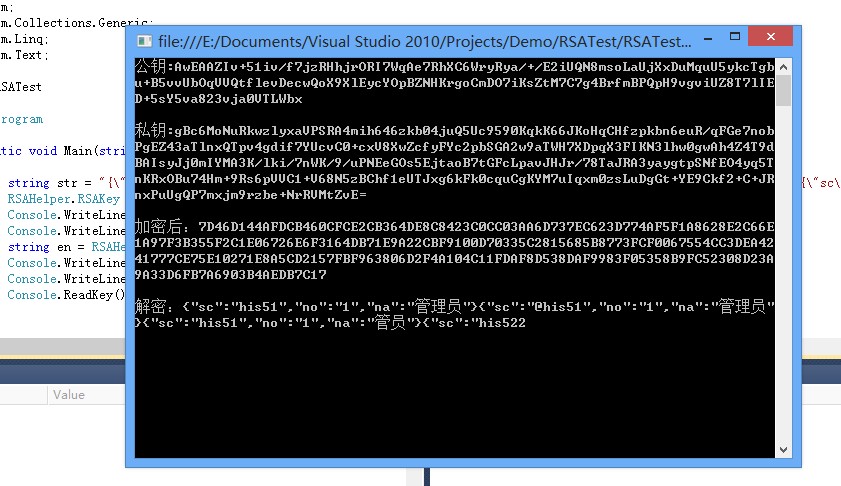
具体的代码解释就不说了 都有注释了,下面给个源码吧,不然片段的代码拼接起来出错概率很高的
在不足之处请大家指导哦,再次感谢csdn和博客园的那两篇非常有用的代码文章
新闻热点
疑难解答