1.2 算法和算法的表示

1.2 算法和算法的表示

1.2.1 算法的概念

1.算法的基本概念

什么是算法？当代著名计算机科学家D.E.Knuth在他撰写的《THE ART OF COMPUTER PROGRAMMING》一书中写到："一个算法，就是一个有穷规则的集合，其中之规则规定了一个解决某一特定类型的问题的运算序列。"简单地说，任何解决问题的过程都是由一定的步骤组成的，把解决问题确定的方法和有限的步骤称作为算法。

需要说明的是，不是只有计算问题才有算法。例如，加工一张写字台，其加工顺序是：桌腿 桌面 抽屉 组装，这就是加工这张写字台的算法。当然，如果是按"抽屉 桌面 桌腿 组装"这样的顺序加工，那就是加工这张写字台有另一种算法，这其中没有计算问题。通常计算机算法分为两大类：数值运算算法和非数值运算算法。数值运算是指对问题求数值解，例如对微分方程求解、对函数的定积分求解、对高次方程求解等，都属于数值运算范围。非数值运算包括非常广泛的领域，例如资料检索、事务管理、数据处理等。数值运算有确定的数学模型，一般都有比较成熟的算法。许多常用算法通常还会被编写成通用程序并汇编成各种程序库的形式，用户需要时可直接调用。例如数学程序库、数学软件包等。而非数值运算的种类繁多，要求不一，很难提供统一规范的算法。在一些关于算法分析的著作中，一般也只是对典型算法作详细讨论，其它更多的非数值运算是需要用户设计其算法的。

下面通过三个简单的问题说明设计算法的思维方法。

例1-1：有黑和蓝两个墨水瓶，但却错把黑墨水装在了蓝墨水瓶子里，而蓝墨水错装在了黑墨水瓶子里，要求将其互换。

算法分析：这是一个非数值运算问题。因为两个瓶子的墨水不能直接交换，所以，解决这一问题的关键是需要引入第三个墨水瓶。设第三个墨水瓶为白色，其交换步骤如下：

① 将黑瓶中的蓝墨水装入白瓶中；② 将蓝瓶中的黑墨水装入黑瓶中；③ 将白瓶中的蓝墨水装入蓝瓶中； ④ 交换结束。

例1-2：计算函数M(x)的值。函数M(x)为：

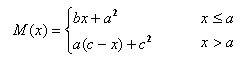算法分析：本题是一个数值运算问题。其中M代表要计算的函数值，有两个不同的表达式，根据x的取值决定采用哪一个算式。根据计算机具有逻辑判断的基本功能，用计算机解题的算法如下：

① 将a、b、c和x的值输入到计算机；

② 判断x≤a?如果条件成立，执行第③步，否则执行第④步；

③ 按表达式bx+a2计算出结果存放到M中，然后执行第⑤步；

④ 按表达式a(c-x)+c3计算出结果存放到M中，然后执行第⑤步；

⑤ 输出M的值；

⑥ 算法结束。

例1-3：给定两个正整数m和n（m≥n），求它们的最大公约数。
　　算法分析：这也是一个数值运算问题，它有成熟的算法，我国数学家秦九韶在《算书九章》一书中曾记载了这个算法。求最大公约数的问题一般用辗转相除法（也称欧几里德算法）求解。
　　例如：设m 35，n 15，余数用r表示。它们的最大公约数的求法如下：
　　35/15商2 余数为5 以n作m，以r作n,继续相除；
　　15/5商3 余数为0 当余数为零时，所得n即为两数的最大公约数。
　　所以35和15两数的最大公约数为5。
　　用这种方法求两数的最大公约数，其算法可以描述如下：
　　① 将两个正整数存放到变量m和n中；
　　② 求余数：计算m除以n，将所得余数存放到变量r中；
　　③ 判断余数是否为0：若余数为0则执行第⑤步，否则执行第④步；
　　④ 更新被除数和余数：将n的值存放到m中，将r的值存放到n中，并转向第②步继续循环执行；
　　⑤输出n的当前值，算法结束。
　　如此循环，直到得到结果。
　　由上述三个简单的例子可以看出，一个算法由若干操作步骤构成，并且这些操作是按一定的控制结构所规定的次序执行。如例1-1中的四个操作步骤是顺序执行的，称之为顺序结构。而在例1-2中，则不是按操作步骤顺序执行，也不是所有步骤都执行。如第三步和第四步的两个操作就不能同时被执行，它们需要根据条件判断决定执行哪个操作，这种结构称之为分支结构。在例1-3中不仅包含了判断，而且需要重复执行。如第二步到第五步之间的步骤就需要根据条件判断是否重复执行，并且一直延续到条件"余数为0"为止，这种具有重复执行功能的结构称之为循环结构。

2.算法的两要素

由上述三个例子可以看出，任何简单或复杂的算法都是由基本功能操作和控制结构这两个要素组成。不论计算机的种类如何之多，但它们最基本的功能操作是一致的。计算机的基本功能操作包括以下四个方面：

(1) 逻辑运算：与、或、非；

(2) 算术运算：加、减、乘、除；

(3) 数据比较：大于、小于、等于、不等于、大于等于、小于等于；

(4) 数据传送：输入、输出、赋值。

算法的控制结构决定了算法的执行顺序。如以上例题所示，算法的基本控制结构通常包括顺序结构、分支结构和循环结构。不论是简单的还是复杂的算法，都是由这三种基本控制结构组合而成的。

算法是对程序控制结构的描述，而数据结构是对程序中数据的描述。因为算法的处理对象必然是问题中所涉及到的相关数据，所以不能离开数据结构去抽象地分析程序的算法，也不能脱离算法去孤立地研究程序的数据结构，而只能从算法和数据结构的统一上去认识程序。但是，在计算机的高级语言中，数据结构是通过数据类型表现的，本书在第三章、第七章、第十章和第十一章中，将通过对C语言数据类型的详细描述说明数据结构在程序设计中的作用。这里我们只讨论算法的问题。

需要强调的是，设计算法与演绎数学有明显区别，演绎数学是以公理系统为基础，通过有限次推演完成对问题的求解。每次推演都是对问题的进一步求解，如此不断推演，直到能将问题的解完全描述出来为止。而设计算法则是充分利用解题环境所提供的基本操作，对输入数据进行逐步加工、变换和处理，从而达到解决问题的目的。