几何平均数是n个变量值连乘积的n次方根。
如果总水平、总成果等于所有阶段、所有环节水平、成果的连乘积总和时,求各阶段、各环节的一般水平、一般成果,要使用几何平均法计算几何平均数。
其特点包括:
(1)几何平均数受极端值的影响较算术平均数小;
(2)如果变量值有负值,计算出的几何平均数就会成为负数或虚数;
(3)它仅适用于具有等比或近似等比关系的数据;
(4)几何平均数的对数是各变量值对数的算术平均数。
要注意的是变量数列中任何一个变量值不能为0,一个为0,则几何平均数为0。
几何平均数要求各观察值之间存在连乘积关系,它的主要用途是:
(1)对比率、指数等进行平均;
(2)计算平均发展速度;
(3)复利下的平均年利率;
(4)连续作业的车间求产品的平均合格率。
(以上内容来自百度百科)
几何平均数分为简单几何平均数和加权几何平均数两种。
(1)简单几何平均数
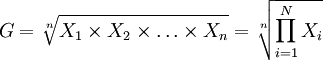
(2)加权几何平均数
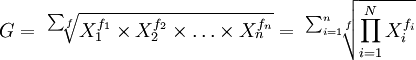
在R的基本函数中,没有提供单独计算几何平均数的函数,但可以通过对算术平均数和加权平均数取对数,可以得到相应的计算结果。
其原理比较简单,假设这里求简单几何平均数,对公式两侧求自然对数,则有:
ln(G) = ln(X1×X2×...×Xn) /n = [ln(X1) + ln(X2) + ... + ln(Xn)] / n
即,取自然对数后,相当于对原变量的对数求算术平均值(在R中求算术平均值的介绍,请参见统计中集中趋势的分析及在R语言中的计算)
则G = eln(G)
即求完原变量的自然对数的均值后,再计算以自然常数e为底,ln(G)为幂的值即可,这在R中可以轻松实现。
(1)例1 已知某市2010~2014年国内生产总值的增长率(以上1年为1)分别为12%、8%、14%、16%和13%,试计算该市5年的平均增长率
编写R程序:
x <- c(12,8,14,16,13)/100
tmp <- mean(log(1+x))
re <- exp(tmp) - 1
print(re)
计算结果为:0.1256843,即平均增长率为12.57%。
(2)例2 某银行的某笔投资按复利计算,在11年中环比增长率:有3年为2%,5年4%,有1年为-2%,有2年为3%,请计算该银行该笔投资年平均增长率。
编写R程序:
x <- c(2,4,-2,3)/100
year <- c(3,5,1,2)
tmp <- weighted.mean(log(1+x),w=year)
re <- exp(tmp) - 1
print(re)
计算结果为:0.02712746,即该笔投资的年平均增长率为:2.71%。
新闻热点
疑难解答