Python中使用递归函数

在一个函数定义中，自己调用自己的编程方法称之为递归（Recursion）。

一、递归简介

一般来说，递归需要有递归前进阶段、递归边界条件和递归返回阶段。当递归条件不满足时，递归前推；当递归条件满足时，递归返回。

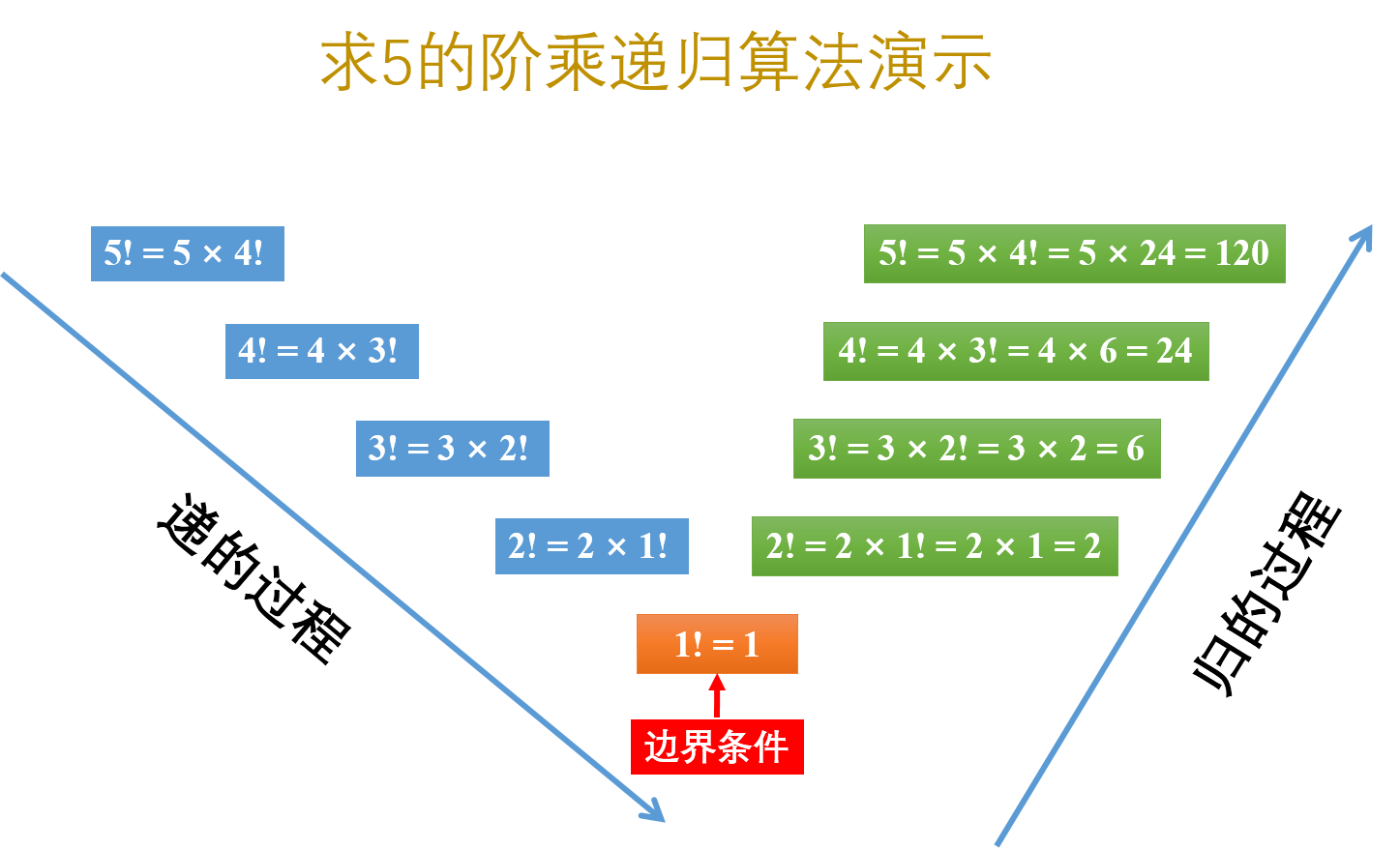
如我们要求5的阶乘（5!），则：

5! = 5 × 4!

我们需要求出4的阶乘后再乘以5就行了，而要求4!：

4! = 4 × 3!

我们需要进一步求出3的阶乘，而

3! = 3 × 2!

我们需要进一步求出2的阶乘，而

2! = 2 × 1!

这时我们知道1的阶乘是1。以上这些步骤就是递归的“前推”过程。

在求出1的阶乘后，我们就知道

2! = 2 × 1! = 2× 1 = 2

则：

3! = 3 × 2! = 3 × 2 = 6

则：

4! = 4 × 3! = 4 × 6 = 24

则：

5! = 5 × 4! = 5 × 24 = 120

这样，我们就得到了5！是120。上面这些步骤就是递归“返回”的过程。

用图表示如下：

二、使用递归方法求一个数的阶乘

#递归法求n!

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n - 1)

result = factorial(5)
print("5！= ", result)
result = factorial(10)
print("10！= ", result)

执行结果如下：

5！= 120
10！= 3628800

三、使用递归方法求斐波那契数列

在前面文章中《Python使用while循环输出斐波那契数列》介绍了斐波那契数列的算法，并给出了几种求斐波那契数列的算法。这里再重新给出一遍。

def Fibonacci(n):
    if n < 0:
        raise IndexError('参数不能小于0。')
    if n == 0:
        return 0
    elif n <= 2:
        return 1
    else:
        return Fibonacci(n - 1) + Fibonacci(n - 2)

for i in range(16):
    print(Fibonacci(i), end = " ")

输出结果如下：

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610

四、使用递归的利弊

使用递归有时使程序更加简洁，减少代码量。但对新手来说，递归比较难以理解，而且使用不当的话，可能使程序无法正常终止。大多数情况下，可以使用循环来替代递归。

本文（完）