python+numpy+matplotalib实现梯度下降法

这个阶段一直在做和梯度一类算法相关的东西，索性在这儿做个汇总，

一、算法论述

梯度下降法(gradient  descent)别名最速下降法（曾经我以为这是两个不同的算法-.-）,是用来求解无约束最优化问题的一种常用算法。下面以求解线性回归为题来叙述：

设：一般的线性回归方程（拟合函数）为：（其中的值为1）

则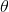这一组向量参数选择的好与坏就需要一个机制来评估，据此我们提出了其损失函数为(选择均方误差)：

我们现在的目的就是使得损失函数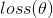取得最小值，即目标函数为：

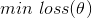
如果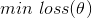的值取到了0，意味着我们构造出了极好的拟合函数，也即选择出了最好的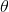值，但这基本是达不到的，我们只能使得其无限的接近于0，当满足一定精度时停止迭代。

那么问题来了如何调整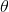使得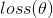取得的值越来越小呢？方法很多，此处以梯度下降法为例：

分为两步：（1）初始化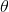的值。

                  （2）改变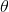的值，使得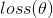按梯度下降的方向减少。

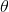值的更新使用如下的方式来完成：

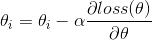
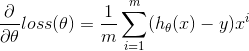
其中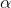为步长因子，这里我们取定值，但注意如果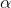取得过小会导致收敛速度过慢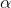，过大则损失函数可能不会收敛，甚至逐渐变大，可以在下述的代码中修改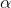的值来进行验证。后面我会再写一篇关于随机梯度下降法的文章，其实与梯度下降法最大的不同就在于一个求和符号。