python素数筛选法浅析

2020-01-04 15:36:16

字体：大中小

来源：转载

供稿：网友

原理：

　　素数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数。在加密应用中起重要的位置，比如广为人知的RSA算法中，就是基于大整数的因式分解难题，寻找两个超大的素数然后相乘作为密钥的。一个比较常见的求素数的办法是埃拉托斯特尼筛法(the Sieve of Eratosthenes) ，说简单一点就是画表格，然后删表格，如图所示：

python,素数,筛选法

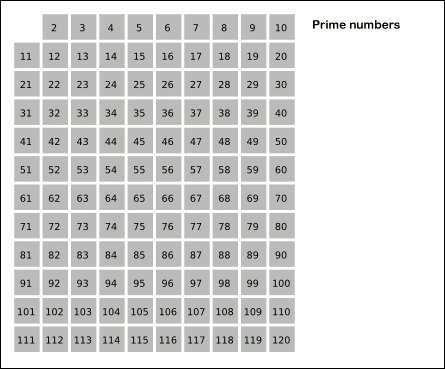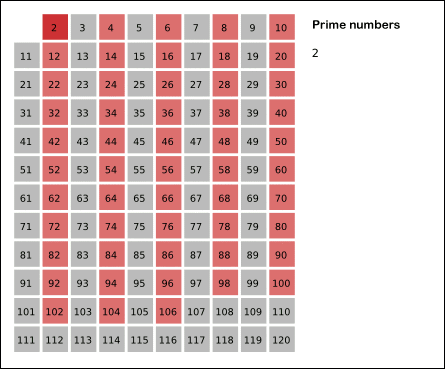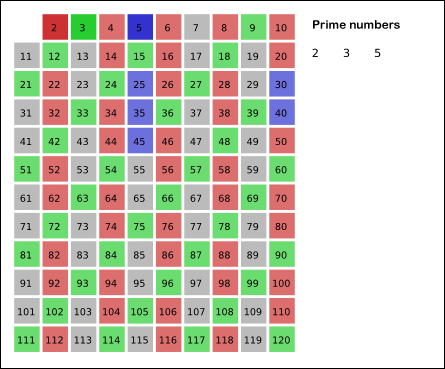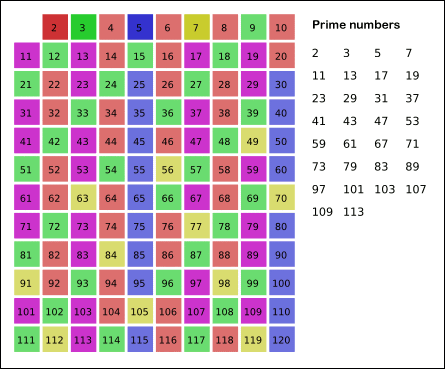
　　从2开始依次往后面数，如果当前数字一个素数，那么就将所有其倍数的数从表中删除或者标记，然后最终得到所有的素数。

有一个优化：

标记2和3的倍数的时候，6被标记了两次。所以从i的平方开始标记，减少很多时间。

比如3的倍数从9开始标记，而不是6，并且每次加6。

除了2以外，所有素数都是奇数。奇数的平方还是奇数，如果再加上奇数就变成了偶数一定不会是素数，所以加偶数(2倍素数)。

预先处理了所有偶数。

注意：1既不是素数也不是合数，这里没有处理1。

#! prime.py import time  def primes(n):  P = []  f = []  for i in range(n+1):   if i > 2 and i%2 == 0:    f.append(1)   else:    f.append(0)   i = 3  while i*i <= n:   if f[i] == 0:    j = i*i    while j <= n:     f[j] = 1     j += i+i   i += 2   P.append(2)  for i in range(3,n,2):   if f[i] == 0:    P.append(i)   return P  def isPrime(n):  if n > 2 and n%2 == 0:   return 0   i = 3  while i*i <= n:   if n%i == 0:    return 0   i += 2   return 1  def primeCnt(n):  cnt = 0  for i in range(2,n):   if isPrime(i):    cnt += 1  return cnt  if __name__ == '__main__':  start = time.clock()  n = 10000000  P = primes(n);  print("There are %d primes less than %d"%(len(P),n))  #for i in range(10):  # print(P[i])  print("Time: %f"%(time.clock()-start))  #for n in range(2,100000):  # if isPrime(n):  #  print("%d is prime"%n)   #print("%d is "%n + ("prime" if isPrime(n) else "not prime"))   start = time.clock()  n = 1000000  print("There are %d primes less than %d"%(primeCnt(n),n))  print("Time: %f"%(time.clock()-start)

用素数筛选法求1千万以内的素数用了5.767s，

普通素数判断法求1百万以内的素数用了9.642s，

用C++素数筛选法求1亿以内的素数用了0.948s，

用C++普通素数判断法求1千万以内的素数用了3.965s，

可见解释语言确实比编译语言慢很多。

附C++程序，用了位压缩优化空间

#include <iostream> #include <cstdio> #include <algorithm> using namespace std; #define N 100000001  unsigned f[(N>>5)+5]; int p[5761456],m; void init() {   int i,j;   for(i=4;i<N;i+=2)     f[i>>5]|=1<<(i&0x1F);   p[m++]=2;   for(i=3;i*i<N;i+=2)     if(!(f[i>>5]&(1<<(i&0x1F))))     {       p[m++]=i;       for(j=i*i;j<N;j+=i+i)         f[j>>5]|=1<<(j&0x1F);     }   for(;i<N;i+=2)     if(!(f[i>>5]&(1<<(i&0x1F))))       p[m++]=i; } int is_prime(int n) {   int i;   for(i=0;p[i]*p[i]<=n;i++)     if(n%p[i]==0)       return 0;   return 1; } int isPrime(int n) {   if(n>2 && n%2==0)     return 0;   int i=3;   while(i*i<=n)   {     if(n%i==0)       return 0;     i+=2;   }   return 1; } int main() {   int n=0,i;   clock_t st=clock();   init();   /*for(i=2;i<10000000;i++)     if(isPrime(i))       n++;*/   printf("%d %dms/n",m,clock()-st);   /*while(~scanf("%d",&n),n)   {     i=lower_bound(p,p+m,n+1)-p;     printf("%d/n",i);   }*/   return 0; }

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持VEVB武林网。

注：相关教程知识阅读请移步到python教程频道。

上一篇：python如何在列表、字典中筛选数据

下一篇：python实现堆和索引堆的代码示例