本文实例讲述了Python基于更相减损术实现求解最大公约数的方法。分享给大家供大家参考,具体如下:
先从网上摘录一段算法的描述如下:
更相减损法:也叫 更相减损术,是出自《 九章算术》的一种求最大公约数的算法,它原本是为 约分而设计的,但它适用于任何需要求最大公约数的场合。
《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。”
翻译成现代语言如下:
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
看完上面的描述,我的第一反应是这个描述是不是有问题?从普适性来说的话,应该是有问题的。举例来说,如果我求解4和4的最大公约数,可半者半之之后,结果肯定错了!后面的算法也不能够进行!
不管怎么说,先实现一下上面的算法描述:
# -*- coding:utf-8 -*-#! python2def MaxCommDivisor(m,n): # even process while m % 2 == 0 and n % 2 == 0: m = m / 2 n = n / 2 # exchange order when needed if m < n: m,n = n,m # calculate the max comm divisor while m - n != n: diff = m - n if diff > n: m = diff else: m = n n = diff return nprint(MaxCommDivisor(55,120))print(MaxCommDivisor(55,77))print(MaxCommDivisor(32,64))print(MaxCommDivisor(16,128))
运行结果:
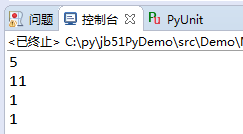
不用说,上面程序执行错误百出。那么该如何更正呢?
首先,除的2最终都应该再算回去!这样,程序修改如下:
def MaxCommDivisor(m,n): com_factor = 1 if m == n: return n else: # process for even number while m % 2 == 0 and n % 2 == 0: m = int(m / 2) n = int(n / 2) com_factor *= 2 if m < n: m,n = n,m diff = m - n while n != diff: m = diff if m < n: m,n = n,m diff = m - n return n * com_factorprint(MaxCommDivisor(55,120))print(MaxCommDivisor(55,77))print(MaxCommDivisor(32,64))print(MaxCommDivisor(16,128))
通过修改,上面程序执行结果如下
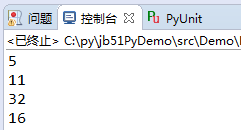
虽说这段程序写出来看着有点怪怪的,但是总体的算法还是实现了。与辗转相除等算法相比,这个在循环的层级上有一定的概率会减小。特别是最后的两组测试数字对儿,这种情况下的效果要好一些。但是,总体上的算法的效率,现在我还不能够给个准确的衡量。
希望本文所述对大家Python程序设计有所帮助。
新闻热点
疑难解答