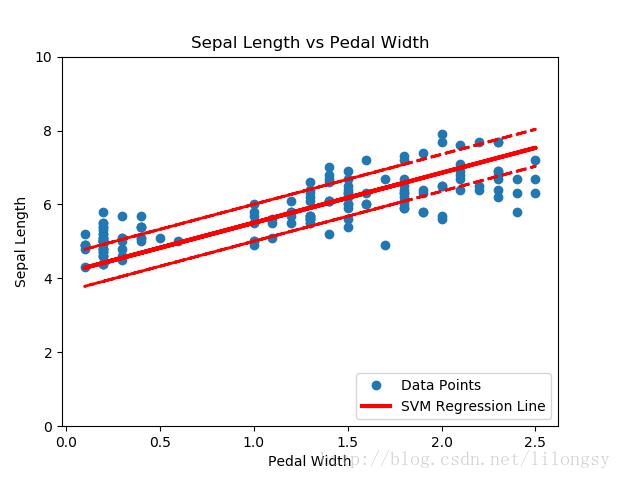
相同的最大间隔(maximum margin)的概念应用到线性回归拟合。代替最大化分割两类目标是,最大化分割包含大部分的数据点(x,y)。我们将用相同的iris数据集,展示用刚才的概念来进行花萼长度与花瓣宽度之间的线性拟合。
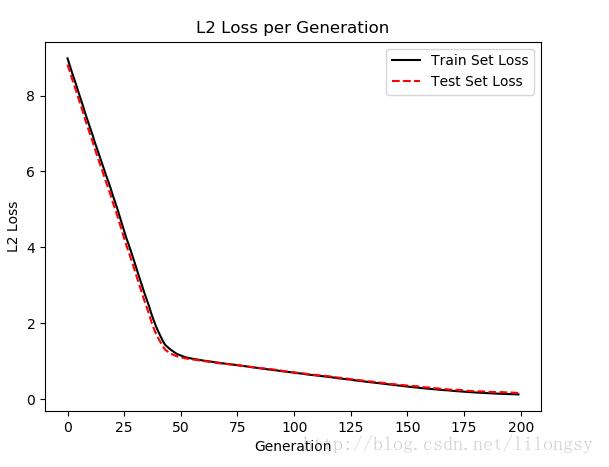
# SVM Regression#----------------------------------## This function shows how to use TensorFlow to# solve support vector regression. We are going# to find the line that has the maximum margin# which INCLUDES as many points as possible## We will use the iris data, specifically:# y = Sepal Length# x = Pedal Widthimport matplotlib.pyplot as pltimport numpy as npimport tensorflow as tffrom sklearn import datasetsfrom tensorflow.python.framework import opsops.reset_default_graph()# Create graphsess = tf.Session()# Load the data# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]iris = datasets.load_iris()x_vals = np.array([x[3] for x in iris.data])y_vals = np.array([y[0] for y in iris.data])# Split data into train/test setstrain_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices)))x_vals_train = x_vals[train_indices]x_vals_test = x_vals[test_indices]y_vals_train = y_vals[train_indices]y_vals_test = y_vals[test_indices]# Declare batch sizebatch_size = 50# Initialize placeholdersx_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)# Create variables for linear regressionA = tf.Variable(tf.random_normal(shape=[1,1]))b = tf.Variable(tf.random_normal(shape=[1,1]))# Declare model operationsmodel_output = tf.add(tf.matmul(x_data, A), b)# Declare loss function# = max(0, abs(target - predicted) + epsilon)# 1/2 margin width parameter = epsilonepsilon = tf.constant([0.5])# Margin term in lossloss = tf.reduce_mean(tf.maximum(0., tf.subtract(tf.abs(tf.subtract(model_output, y_target)), epsilon)))# Declare optimizermy_opt = tf.train.GradientDescentOptimizer(0.075)train_step = my_opt.minimize(loss)# Initialize variablesinit = tf.global_variables_initializer()sess.run(init)# Training looptrain_loss = []test_loss = []for i in range(200): rand_index = np.random.choice(len(x_vals_train), size=batch_size) rand_x = np.transpose([x_vals_train[rand_index]]) rand_y = np.transpose([y_vals_train[rand_index]]) sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_train_loss = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_train]), y_target: np.transpose([y_vals_train])}) train_loss.append(temp_train_loss) temp_test_loss = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_test]), y_target: np.transpose([y_vals_test])}) test_loss.append(temp_test_loss) if (i+1)%50==0: print('-----------') print('Generation: ' + str(i+1)) print('A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b))) print('Train Loss = ' + str(temp_train_loss)) print('Test Loss = ' + str(temp_test_loss))# Extract Coefficients[[slope]] = sess.run(A)[[y_intercept]] = sess.run(b)[width] = sess.run(epsilon)# Get best fit linebest_fit = []best_fit_upper = []best_fit_lower = []for i in x_vals: best_fit.append(slope*i+y_intercept) best_fit_upper.append(slope*i+y_intercept+width) best_fit_lower.append(slope*i+y_intercept-width)# Plot fit with dataplt.plot(x_vals, y_vals, 'o', label='Data Points')plt.plot(x_vals, best_fit, 'r-', label='SVM Regression Line', linewidth=3)plt.plot(x_vals, best_fit_upper, 'r--', linewidth=2)plt.plot(x_vals, best_fit_lower, 'r--', linewidth=2)plt.ylim([0, 10])plt.legend(loc='lower right')plt.title('Sepal Length vs Pedal Width')plt.xlabel('Pedal Width')plt.ylabel('Sepal Length')plt.show()# Plot loss over timeplt.plot(train_loss, 'k-', label='Train Set Loss')plt.plot(test_loss, 'r--', label='Test Set Loss')plt.title('L2 Loss per Generation')plt.xlabel('Generation')plt.ylabel('L2 Loss')plt.legend(loc='upper right')plt.show() 直观地讲,我们认为SVM回归算法试图把更多的数据点拟合到直线两边2ε宽度的间隔内。这时拟合的直线对于ε参数更有意义。如果选择太小的ε值,SVM回归算法在间隔宽度内不能拟合更多的数据点;如果选择太大的ε值,将有许多条直线能够在间隔宽度内拟合所有的数据点。作者更倾向于选取更小的ε值,因为在间隔宽度附近的数据点比远处的数据点贡献更少的损失。