神经网络在机器学习中有很大的应用,甚至涉及到方方面面。本文主要是简单介绍一下神经网络的基本理论概念和推算。同时也会介绍一下神经网络在数据分类方面的应用。
首先,当我们建立一个回归和分类模型的时候,无论是用最小二乘法(OLS)还是最大似然值(MLE)都用来使得残差达到最小。因此我们在建立模型的时候,都会有一个loss function。
而在神经网络里也不例外,也有个类似的loss function。
对回归而言:
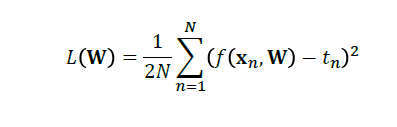
对分类而言:
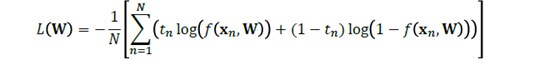
然后同样方法,对于W开始求导,求导为零就可以求出极值来。
关于式子中的W。我们在这里以三层的神经网络为例。先介绍一下神经网络的相关参数。
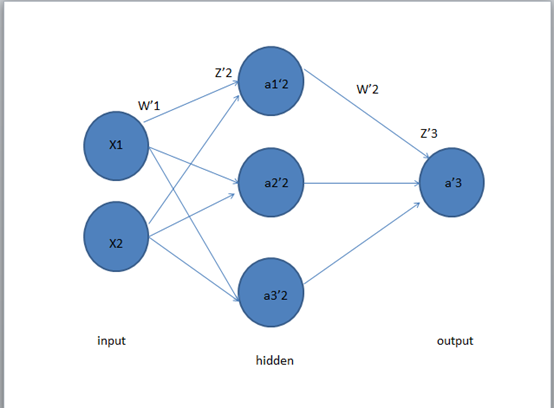
第一层是输入层,第二层是隐藏层,第三层是输出层。
在X1,X2经过W1的加权后,达到隐藏层,然后经过W2的加权,到达输出层
其中,
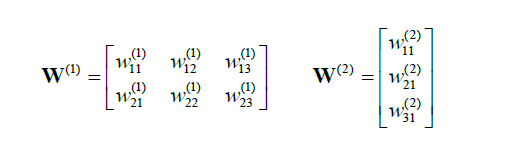
我们有:
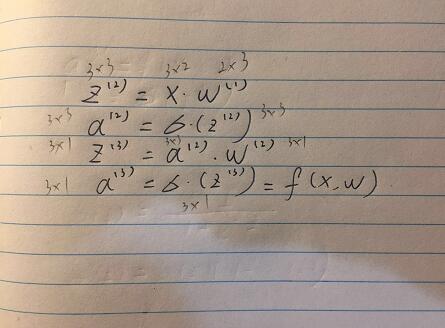
至此,我们建立了一个初级的三层神经网络。
当我们要求其的loss function最小时,我们需要逆向来求,也就是所谓的backpropagation。
我们要分别对W1和W2进行求导,然后求出其极值。
从右手边开始逆推,首先对W2进行求导。
代入损失函数公式:
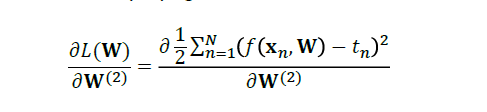
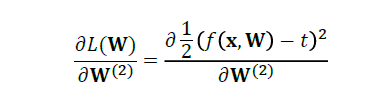
然后,我们进行化简:
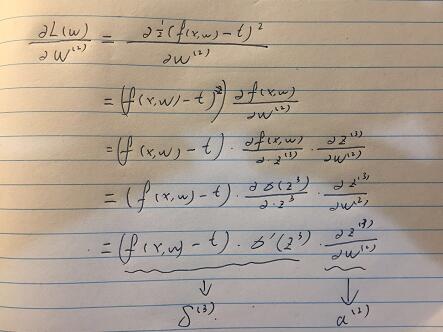
化简到这里,我们同理再对W1进行求导。
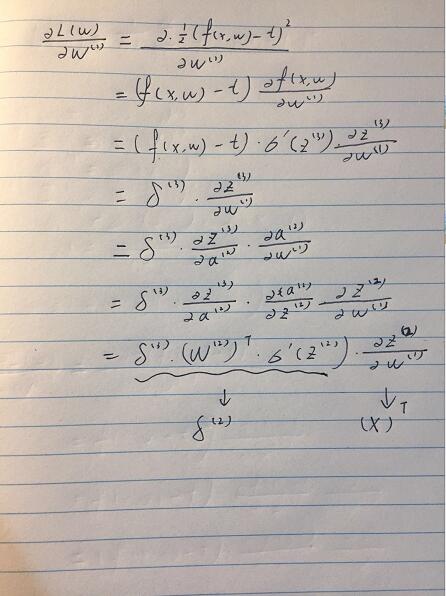
我们可以发现当我们在做bp网络时候,有一个逆推回去的误差项,其决定了loss function 的最终大小。
在实际的运算当中,我们会用到梯度求解,来求出极值点。
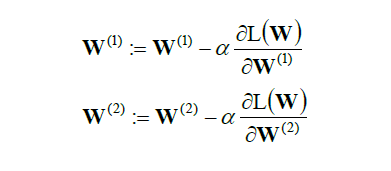
总结一下来说,我们使用向前推进来理顺神经网络做到回归分类等模型。而向后推进来计算他的损失函数,使得参数W有一个最优解。
当然,和线性回归等模型相类似的是,我们也可以加上正则化的项来对W参数进行约束,以免使得模型的偏差太小,而导致在测试集的表现不佳。
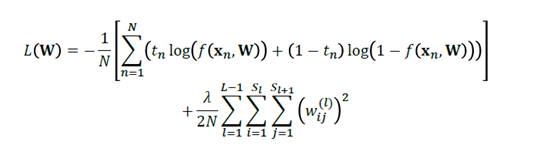
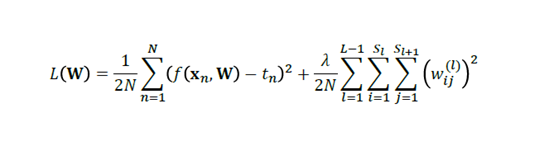
Python 的实现:
使用了KERAS的库
解决线性回归:
model.add(Dense(1, input_dim=n_features, activation='linear', use_bias=True))# Use mean squared error for the loss metric and use the ADAM backprop algorithmmodel.compile(loss='mean_squared_error', optimizer='adam')# Train the network (learn the weights)# We need to convert from DataFrame to NumpyArrayhistory = model.fit(X_train.values, y_train.values, epochs=100, batch_size=1, verbose=2, validation_split=0)
解决多重分类问题:
# create modelmodel = Sequential()model.add(Dense(64, activation='relu', input_dim=n_features))model.add(Dropout(0.5))model.add(Dense(64, activation='relu'))model.add(Dropout(0.5))# Softmax output layermodel.add(Dense(7, activation='softmax'))model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])model.fit(X_train.values, y_train.values, epochs=20, batch_size=16)y_pred = model.predict(X_test.values)y_te = np.argmax(y_test.values, axis = 1)y_pr = np.argmax(y_pred, axis = 1)print(np.unique(y_pr))print(classification_report(y_te, y_pr))print(confusion_matrix(y_te, y_pr))
当我们选取最优参数时候,有很多种解决的途径。这里就介绍一种是gridsearchcv的方法,这是一种暴力检索的方法,遍历所有的设定参数来求得最优参数。
from sklearn.model_selection import GridSearchCVdef create_model(optimizer='rmsprop'): model = Sequential() model.add(Dense(64, activation='relu', input_dim=n_features)) model.add(Dropout(0.5)) model.add(Dense(64, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(7, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy']) return modelmodel = KerasClassifier(build_fn=create_model, verbose=0)optimizers = ['rmsprop']epochs = [5, 10, 15]batches = [128]param_grid = dict(optimizer=optimizers, epochs=epochs, batch_size=batches, verbose=['2'])grid = GridSearchCV(estimator=model, param_grid=param_grid)grid.fit(X_train.values, y_train.values)
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持VEVB武林网。
注:相关教程知识阅读请移步到python教程频道。