sympy版本:1.2
假设求解矩阵方程
AX=A+2X
其中
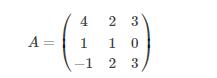
求解之前对矩阵方程化简为
(A−2E)X=A
令
B=(A−2E)
使用qtconsole输入下面程序进行求解
In [26]: from sympy import *In [27]: from sympy.abc import *In [28]: A=Matrix([[4,2,3],[1,1,0],[-1,2,3]])In [29]: AOut[29]: Matrix([[ 4, 2, 3],[ 1, 1, 0],[-1, 2, 3]])In [30]: B=A-2*diag(1,1,1)In [31]: BOut[31]: Matrix([[ 2, 2, 3],[ 1, -1, 0],[-1, 2, 1]])In [32]: B.inv()*AOut[32]: Matrix([[ 3, -8, -6],[ 2, -9, -6],[-2, 12, 9]])
将结果验证一下:
In [38]: X=B.inv()*AIn [39]: XOut[39]: Matrix([[ 3, -8, -6],[ 2, -9, -6],[-2, 12, 9]])In [40]: A*X-A-2*XOut[40]: Matrix([[0, 0, 0],[0, 0, 0],[0, 0, 0]])
求解矩阵方程过程中注意的问题是左乘还是右乘问题,在此例中是B.inv()*A ,如果矩阵方程变为
XA=A+2X
那么求解结果为:
In [35]: X=A*B.inv()In [36]: XOut[36]: Matrix([[ 3, -8, -6],[ 2, -9, -6],[-2, 12, 9]])
将结果验证一下:
X=A*B.inv()XOut[36]: Matrix([[ 3, -8, -6],[ 2, -9, -6],[-2, 12, 9]])X*A-A-2*XOut[37]: Matrix([[0, 0, 0],[0, 0, 0],[0, 0, 0]])
以上这篇python/sympy求解矩阵方程的方法就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持VEVB武林网。
注:相关教程知识阅读请移步到python教程频道。