标签: 杂谈 | 分类: 嵌入式 |
卷积这个东东是“信号与系统”中论述系统对输入信号的响应而提出的。因为是对模拟信号论述的,所
以常常带有繁琐的算术推倒,很简单的问题的本质常常就被一大堆公式淹没了,那么卷积究竟物理意义
怎么样呢?
卷积表示为y(n) = x(n)*h(n)
使用离散数列来理解卷积会更形象一点,我们把y(n)的序列表示成y(0),y(1),y(2) and so on; 这是系
统响应出来的信号。
同理,x(n)的对应时刻的序列为x(0),x(1),x(2)...and so on;
其实我们如果没有学过信号与系统,就常识来讲,系统的响应不仅与当前时刻系统的输入有关,也跟之
前若干时刻的输入有关,因为我们可以理解为这是之前时刻的输入信号经过一种过程(这种过程可以是
递减,削弱,或其他)对现在时刻系统输出的影响,那么显然,我们计算系统输出时就必须考虑现在时
刻的信号输入的响应以及之前若干时刻信号输入的响应之“残留”影响的一个叠加效果。
假设0时刻系统响应为y(0),若其在1时刻时,此种响应未改变,则1时刻的响应就变成了y(0)+y(1),叫序
列的累加和(与序列的和不一样)。但常常系统中不是这样的,因为0时刻的响应不太可能在1时刻仍旧
未变化,那么怎么表述这种变化呢,就通过h(t)这个响应函数与x(0)相乘来表述,表述为x(m)×h(m-n)
,具体表达式不用多管,只要记着有大概这种关系,引入这个函数就能够表述y(0)在1时刻究竟削弱了多
少,然后削弱后的值才是y(0)在1时刻的真实值,再通过累加和运算,才得到真实的系统响应。
再拓展点,某时刻的系统响应往往不一定是由当前时刻和前一时刻这两个响应决定的,也可能是再加上
前前时刻,前前前时刻,前前前前时刻,等等,那么怎么约束这个范围呢,就是通过对h(n)这个函数在
表达式中变化后的h(m-n)中的m的范围来约束的。即说白了,就是当前时刻的系统响应与多少个之前时刻
的响应的“残留影响”有关。
当考虑这些因素后,就可以描述成一个系统响应了,而这些因素通过一个表达式(卷积)即描述出来不
得不说是数学的巧妙和迷人之处了。
==================================================================================================
对于非数学系学生来说,只要懂怎么用卷积就可以了,研究什么是卷积其实意义不大,它就是一种微元相
乘累加的极限形式。卷积本身不过就是一种数学运算而已。就跟“蝶形运算”一样,怎么证明,这是数
学系的人的工作。在信号与系统里,f(t)的零状态响应y(t)可用f(t)与其单位冲激响应h(t) 的卷积积分求解得,即y(t)
=f(t)*h(t)。学过信号与系统的都应该知道,时域的卷积等于频域的乘积,即有 Y(s)=F(s)×H(s)。
(s=jw,拉氏变换后等到的函数其实就是信号的频域表达式)有一点你必须明白,在通信系统里,我们关心的以及 要研究的是信号的频域,不是时域,原因是因为信
号的频率是携带有信息的量。所以,我们需要的是Y(s)这个表达式,但是实际上,我们往往不能很容易的得到F(s)和H(s)这两个表达
式,但是能直接的很容易的得到f(t)和h(t),所以为了找到Y(s)和y(t)的对应关系,就要用到卷积运算
。复频域。s=jw,当中的j是复数单位,所以使用的是复频域。通俗的解释方法是,因为系统中有电感X=jwL、电容
X=1/jwC,物理意义是,系统H(s)对不同的频率分量有不同的衰减,即这种衰减是发生在频域的,所以为
了与时域区别,引入复数的运算。但是在复频域计算的形式仍然满足欧姆定理、KCL、KVL、叠加法。负的频率。之所以会出现负的频率,这只是数学运算的结果,只存在于数学运算 中,实际中不会有负的频率。
卷积的过程就是相当于把信号分解为无穷多的冲击信号,然后进行冲击响应的叠加。
回家,以示爱民如子。
有一个无赖,想出人头地却没啥指望,心想:既然扬不了善名,出恶名也成啊。怎么出恶名?炒作呗!
怎么炒作?找名人呀!他自然想到了他的行政长官——县令。
无赖于是光天化日之下,站在县衙门前撒了一泡尿,后果是可想而知地,自然被请进大堂挨了一板子,
然后昂首挺胸回家,躺了一天,嘿!身上啥事也没有!第二天如法炮制,全然不顾行政长管的仁慈和衙
门的体面,第三天、第四天......每天去县衙门领一个板子回来,还喜气洋洋地,坚持一个月之久!这
无赖的名气已经和衙门口的臭气一样,传遍八方了!
县令大人噤着鼻子,呆呆地盯着案子上的惊堂木,拧着眉头思考一个问题:这三十个大板子怎么不好使
捏?......想当初,本老爷金榜题名时,数学可是得了满分,今天好歹要解决这个问题:
——人(系统!)挨板子(脉冲!)以后,会有什么表现(输出!)?
——费话,疼呗!
——我问的是:会有什么表现?
——看疼到啥程度。像这无赖的体格,每天挨一个板子啥事都不会有,连哼一下都不可能,你也看到他
那得意洋洋的嘴脸了(输出0);如果一次连揍他十个板子,他可能会皱皱眉头,咬咬牙,硬挺着不哼(
输出1);揍到二十个板子,他会疼得脸部扭曲,象猪似地哼哼(输出3);揍到三十个板子,他可能会
象驴似地嚎叫,一把鼻涕一把泪地求你饶他一命(输出5);揍到四十个板子,他会大小便失禁,勉强哼
出声来(输出1);揍到五十个板子,他连哼一下都不可能(输出0)—— 死啦!
县令铺开坐标纸,以打板子的个数作为X轴,以哼哼的程度(输出)为Y轴,绘制了一条曲线:
——呜呼呀!这曲线象一座高山,弄不懂弄不懂。为啥那个无赖连挨了三十天大板却不喊绕命呀?
——呵呵,你打一次的时间间隔(Δτ=24小时)太长了,所以那个无赖承受的痛苦程度一天一利索,没
有叠加,始终是一个常数;如果缩短打板子的时间间隔(建议Δτ=0.5秒),那他的痛苦程度可就迅速
叠加了;等到这无赖挨三十个大板(t=30)时,痛苦程度达到了他能喊叫的极限,会收到最好的惩戒效
果,再多打就显示不出您的仁慈了。
——还是不太明白,时间间隔小,为什么痛苦程度会叠加呢?
——这与人(线性时不变系统)对板子(脉冲、输入、激励)的响应有关。什么是响应?人挨一个板子
后,疼痛的感觉会在一天(假设的,因人而异)内慢慢消失(衰减),而不可能突然消失。这样一来,
只要打板子的时间间隔很小,每一个板子引起的疼痛都来不及完全衰减,都会对最终的痛苦程度有不同
的贡献:
t个大板子造成的痛苦程度=Σ(第τ个大板子引起的痛苦*衰减系数)[衰减系数是(t-τ)的函数,仔细
品味]
数学表达为:y(t)=∫T(τ)H(t-τ)
——拿人的痛苦来说卷积的事,太残忍了。除了人以外,其他事物也符合这条规律吗?
——呵呵,县令大人毕竟仁慈。其实除人之外,很多事情也遵循此道。好好想一想,铁丝为什么弯曲一
次不折,快速弯曲多次却会轻易折掉呢?
——恩,一时还弄不清,容本官慢慢想来——但有一点是明确地——来人啊,将撒尿的那个无赖抓来,
狠打40大板!
作者:果程C链接:https://www.zhihu.com/question/22298352/answer/50940942来源:知乎著作权归作者所有,转载请联系作者获得授权。对于初学者,我推荐用复利的例子来理解卷积可能更好理解一些:小明存入100元钱,年利率是5%,按复利计算(即将每一年所获利息加入本金,以计算下一年的利息),那么在五年之后他能拿到的钱数是 将这笔钱存入银行的一年之后,小明又往银行中存入了100元钱,年利率仍为5%,那么这笔钱按复利计算,到了第五年,将收回的钱数是
将这笔钱存入银行的一年之后,小明又往银行中存入了100元钱,年利率仍为5%,那么这笔钱按复利计算,到了第五年,将收回的钱数是 以此类推,如果小明每年都往银行中存入新的100元钱,那么这个收益表格将是这样的:<img src="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_b.jpg" data-rawwidth="1296" data-rawheight="284" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_r.jpg">可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即:
以此类推,如果小明每年都往银行中存入新的100元钱,那么这个收益表格将是这样的:<img src="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_b.jpg" data-rawwidth="1296" data-rawheight="284" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_r.jpg">可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即: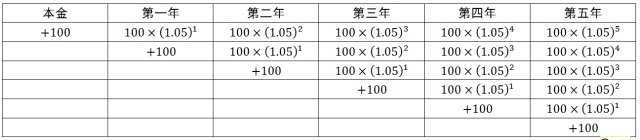 可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即:<img src="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_b.jpg" data-rawwidth="1077" data-rawheight="124" class="origin_image zh-lightbox-thumb" width="1077" data-original="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_r.jpg">用求和符号来简化这个公式,可以得到:
可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即:<img src="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_b.jpg" data-rawwidth="1077" data-rawheight="124" class="origin_image zh-lightbox-thumb" width="1077" data-original="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_r.jpg">用求和符号来简化这个公式,可以得到: 用求和符号来简化这个公式,可以得到:
用求和符号来简化这个公式,可以得到: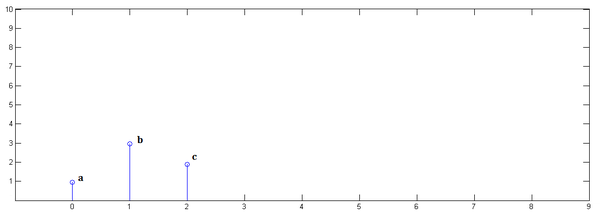 已知
已知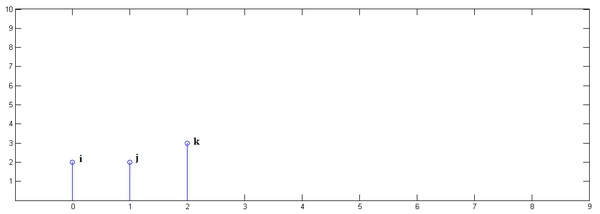 下面通过演示求
下面通过演示求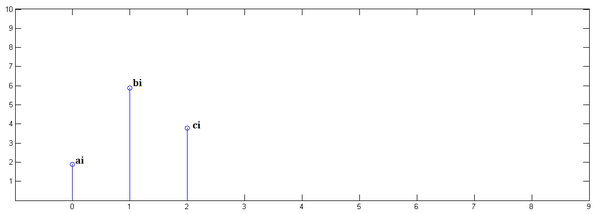 第二步,
第二步,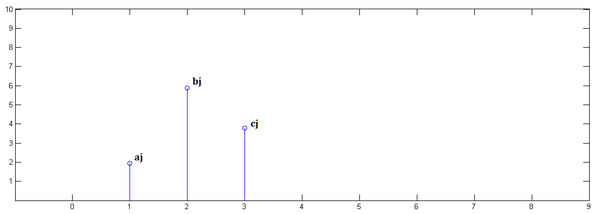 第三步,
第三步,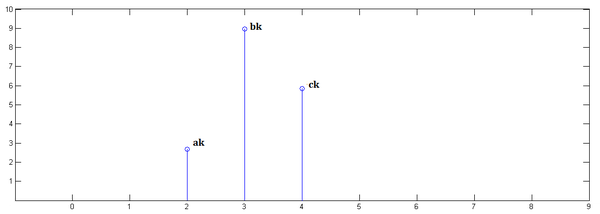 最后,把上面三个图叠加,就得到了
最后,把上面三个图叠加,就得到了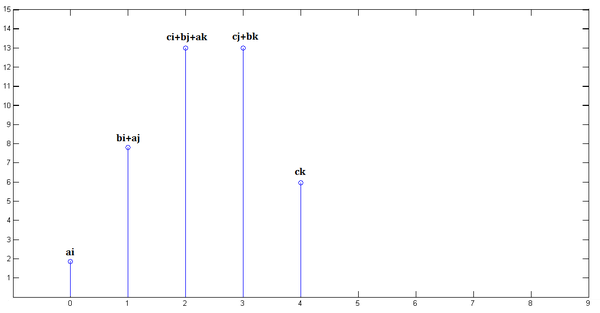 简单吧?无非是平移(没有反褶!)、叠加。====================================================从这里,可以看到卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数(如:输入信号)上的加权叠加。重复一遍,这就是卷积的意义:加权叠加。对于线性时不变系统,如果知道该系统的单位响应,那么将单位响应和输入信号求卷积,就相当于把输入信号的各个时间点的单位响应 加权叠加,就直接得到了输出信号。通俗的说:在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。这正是单位响应是如此重要的原因。在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。这正是单位响应是如此重要的原因。在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。这正是单位响应是如此重要的原因。
简单吧?无非是平移(没有反褶!)、叠加。====================================================从这里,可以看到卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数(如:输入信号)上的加权叠加。重复一遍,这就是卷积的意义:加权叠加。对于线性时不变系统,如果知道该系统的单位响应,那么将单位响应和输入信号求卷积,就相当于把输入信号的各个时间点的单位响应 加权叠加,就直接得到了输出信号。通俗的说:在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。这正是单位响应是如此重要的原因。在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。这正是单位响应是如此重要的原因。在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。这正是单位响应是如此重要的原因。新闻热点
疑难解答