原著:fahad gilani
翻译:yy2better
原文出处:msdn magazine march 2004(c# in-depth)
下载此文章的代码 scientificc.exe (127kb)
本文假定你熟悉 c#  摘要
摘要
c#语言在多种项目中应用的相当成功,它们包括 web、数据库、gui及其他更多类型项目。有充分理由认为,c# 代码最前沿的应用领域之一很可能是科学计算。但 c# 能达到 fortran 和 c++ 应用于科学计算项目的水平吗?
在本文中,通过研究由 .net 通用语言运行时决定的 jit 编译器、微软中间语言和垃圾收集器如何影响性能,作者回答了这个问题。他还论述了 c# 数据类型,包括数组和矩阵,及其它在科学计算 应用中起重要作用的语言特性。
c#语言已获得工作在不同领域开发者的尊敬并在他们中间得到相当的普及。最近两年,c# 在交付健壮的产品中起着重要的作用,从桌面应用程序到 web 服务,从高阶商务自动化到系统级应用程序,从单用户产品到网络分布环境中的企业解决方案,都有 c# 的存在。假设此语言的强大特性,你可能会问 c# 和 microsoft®.net 框架是否能被 更加广泛地用于除gui和基于web组件之外的程序中。它是否已准备好被科学团体用于开发高性能数字性编码?
答案并不一目了然,因为首先需要回答一些其它问题。例如,什么是科学性计算(scientific computing)?为什么它不同于传统的计算?语言是否真的具备适于科学计算 编程的特性?
本文中,我会揭示 c# 的一些内在特性,它们允许开发者以轻松、实用的方式使用注重性能(performance-critical)的代码。你将看到 c# 如何在科学 社区中扮演着重要角色,如何为下一代数字计算敞开大门。你也将看到,尽管谣传因内存管理开销过大而使受管代码运行缓慢,但是复杂性适度的代码运行得很快;它根本不会被垃圾收集器中断,因为大多数数字上的处理不会需要足够多的内存释放而导致调用垃圾收集。我将探究 c# 在数字计算世界里是不是一个好的选择。我还将考察一些基准(benchmark),并将结果与非受管 c++ 代码进行比较以便了解在性能和效率方面 c# 处在什么位置。  计算科学
计算科学
计算机的可用性已经使科学家们更容易地证明理论、解答复杂方程式、模拟3d环境、预报天气和执行许多其它高强度运算任务。多年来,数百种高级语言被研发出来以促进计算机在这些领域的应用(其中 有些是高度专业的并发设计概念框架,例如 ada和 occam;有些是昙花一现的计算机科学工具,例如 eiffel 或 algol)。然而,有少数成为卓越的科学性编程语言,例如 c、c++ 和 fortran——它们在当今科学计算领域扮演 着主要角色已有相当长的一段时间。
但是,如何确定哪种高级语言用于科学计算呢?一般来说,某种语言要想有资格成为产生科学计算代码的平台,它必须包括的标准之一是提供一套丰富的能被用于衡量性能的工具 ,并且必须允许开发者轻松有效地表达问题域。本质上,科学计算语言应该能生成可以被细微调整的有效的高性能代码。  性能和语言
性能和语言
性能已经成为区分用于科学计算编程语言的关键因素之一。编译器和代码生成技术常常被认为是性能限制因素,但这种假定不完全正确。例如,使用最广泛的 c++ 编译器在代码生成和优化方面做得很好。 有一些微妙之处,它们与代码的效率比起来,通常就不重要了。例如,c++中应避免创建过多临时对象,尤其它是一种非常容易创建未命名临时变量但又不使用它们的语言。可以使用表达式模板达到此目的,表达式模板允许延迟数学表达式的实际运算,直到它被赋值。结果可以避免在运行时招致 巨大的抽象惩罚(abstraction penalty)。
这不是说语言特性是影响性能的唯一因素。当进行语言之间明确的评估以衡量性能和成本时,真正评估的是编译器编写者的技巧,而不是语言本身。如果能从语言、运行时或平台中获取可接 受的性能,那么选择可能紧紧关乎个人所好。
如果你已经体验过 c# 并且正在考虑进行真正的科学计算,那么没必要采用其它语言;c# 绰绰有余。  msil和可移植性
msil和可移植性
与所有其它面向.net的语言一样,c# 编译成微软中间语言(msil),它运行于通用语言运行时(clr)。clr 可松散地被描述为just-in-time(jit)优化编译器和垃圾收集器 的混合物。c# 公开和利用了clr中的很多功能,所以更细致地研究该运行时的工作机制是很重要的。
科学家的关键需求之一是代码可移植性。科学研究机构和实验室拥有许多平台和机器,包括基于 unix 工作站和pc。它们常常希望在不同机器上运行代码,以追求更好的结果或因为 某一特定的机器为他们提供一套数据处理和分析工具。然而,达到完全的硬件透明度已不是一个轻松的任务而且不总是完全可能。例如,多数大规模项目开发时使用了多种语言混合 的方法;因此,很难保证在一种架构或平台上可运行的应用程序也能在另一种上运行。
clr 使应用程序和库可被多种语言编写,这些语言都可编译成 msil。然后msil可运行在任何支持它的架构上。现在,科学家就可用 fortran 编写它们数学库,在c++中调用它们,使用 c# 和 asp.net 在 internet 发布结果。
不像 java 虚拟机(jvm),clr是一个常规用途环境,它被设计用来面向多种不同的编程语言。此外,clr 提供了数据层,不仅仅是应用层的互用性并允许在语言间共享资源。
目前,可以获得大量能输出 msil 的语言编译器。这些语言包括(但不限于)ada、c、c++caml、cobol、eiffel、fortran、java、list、logo、mixal、pascal、perl、php、python、scheme 和 smalltalk。另外,system.reflection.emit 名字空间大大降低了开发 面向 clr 的编译器的进入门槛。
将 clr 移植到不同架构是一项正在进行的工作。然而,一份开源实现已由 mono/ximian 开发出来,并且可获得 s390、sparc 和 powerpc 架构 以及 strongarm 系统的实现。微软也发布了一个运行在 freebsd 系统上的开源版本,包括 mac os x。(更多信息请看 msdn 杂志 2002 july 上 jason wittington 的文章 "rotor: shared source cli provides source code for a freebsd implementation of .net")
所有这些进展发生在过去的仅仅数年中。假以更多时间,很可能一个全功能的 clr 将可以适用于所有通用架构。  jit 编译器是否变得更好?
jit 编译器是否变得更好?
jit 编译技术是一种非凡的技术,它为广泛的优化敞开了大门。 尽管当前实现的实际情况是:由于时间限制,能被完成的优化在数量上是限制性的,从理论上讲,它应该比现有的任何静态编译器做得要好。当然 ,这是因为注重性能的代码的动态属性或其上下文直到运行时才被充分了解或被验证。jit 编译器能通过生成更有效代码来使用这些收集的信息,从理论上讲,这些代码每次运行都会被再次优化。通常,编译器为每个方法只发出一次机器码。一旦机器码生成,它就以原始机器速度执行。
在科学计算编程中,这可能是一个便利的工具。科学性代码主要由数字和用数字表示的算法组成。要在合理的时间内完成这些计算,某些硬件资源需要被细心利用。虽然一些静态编译器在优化代码方面做得很好,但是 jit 编译器的动态 本性允许使用众多技术优化资源利用,譬如基于优先级的注册配置,懒代码选择,缓存调整和特定 cpu 优化。这些技术也为更严格的优化提供了广袤的空间,譬如 强度缩量(strength reduction)和常量繁殖(constant propagation)、冗余 的存储后加载(load-after-store)、公共子表达式排除、数组边界检查排除、方法内联等等。虽然 jit 编译器有可能实现这些类型的优化,但当前.net jit编译器没有 先进到这一步。
过去,程序员要确保运行在某种机器上的代码是为底层体系架构进行过手工优化(例如软件流水线,或手工利用缓存),此乃惯例。在另一台不同硬件机器上运行同样的代码需要修改原始代码以对应新硬件。随着时间的流逝,处理器执行代码的方式 已经有所改变,它们使用专门的内置指令或技术。这些优化现在能通过 jit 编译器发掘出来,不需要修改现有代码。结果,运行在工作站上的代码也可以在具有完全不同 体系架构的家庭 pc 上运行得一样好。
.net框架1.1版本发布的 jit 编译器相对于它的前辈 1.0 版本有相当的改进。figure 1显示 clr1.0 和 1.1 版本的执行比较,它是通过在两个平台上运行 scimark2.0 基准套件得出的。测试机器配置是 奔腾四 2.4ghz,256兆内存。 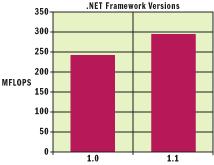
figure 1 .net 1.1中 jit 的改进
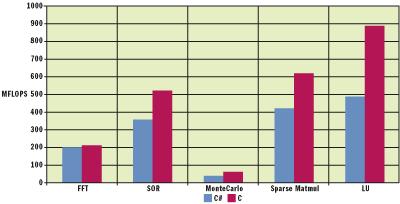
scimark 基准由许多在科学计算应用中建立的通用计算要素组成,在内存访问浮点运算方面各自处理不同的行为模式。这些要素是:快速傅立叶转换(fft)、连续 松弛迭代(sor:over-relaxation iterations)、用于复杂线性系统的解决方案的蒙特-卡罗积分、稀疏矩阵乘法和稠密矩阵分解(lu) 。
scimark 最初用 java 开发(http://math.nist.gov/scimark),后来被 chris re 和 wener vogels 移植到 c#(http://math.nist.gov/scimark)。注意这个实现没有使用不安全代码,这会使它运行速度提高 5 至 10 个百分点。
figure 1 以每秒百万浮点运算数(mflops)显示了.net框架两个版本的综合得分。这给你一个大致的概念:当前版本(1.1) 运行得如何 以及未来版本改进得将有多好。
此图显示公共语言运行时 1.1 版本胜过 1.0 版本一大截(具体在这里是 54.1 mflops )。版本 1.1 在整个实现中融进了许多性能改进技术,包括一些已加入 jit 编译器中的针对特定架构 的优化,譬如使用 ia-32 sse2 指令进行浮点数到整数转换。当然,编译器也对其它处理器生成对应的优化代码。
我期待下一次发布的 jit 编译器将表现更佳。jit 编译器将产生比静态编译器更快的运行代码,这只是时间问题。  自动内存管理
自动内存管理
从实现角度看,自动内存管理大概是 clr 给开发者最好的礼物。与 c/c++ malloc 或 new 调用中缓慢且昂贵的链表横断式释放相比,crl 的内存分配相对较快(堆指针仅仅被移动到下一个空闲槽)。而且,内存在运行时是自动管理的,例如自动释放和整理未使用空间。程序师不再需要追踪指针、过早释放内存块或根本不释放它们(虽然像 c# 和 visual c++® 这样的语言仍赋予开发者那样的选择)。
几乎可预见的是,许多开发者对考虑使用垃圾收集器的反应。然而,对于使用内存频繁的应用程序,垃圾收集器确实导致小小的运行时成本,它们还处理所有跟踪内存泄漏 的凌乱细节以及清除摇摆指针。它们始终保持对堆资源的管理、使其紧凑并可以重复利用。
最近的研究和试验显示,在计算密集型应用中,对象的分配和释放更加频繁,垃圾收集器通过堆压塑实际上可以提高性能。另外,内存中以不同方式随机展开的被频繁引用的对象被紧凑地收集在一起以 便提供更佳的定位和缓冲利用。这大大加速了整个应用程序的性能。同时,垃圾收集器的缺点之一是其不可预测的时间性,这导致很难使收集工作只在正确的时刻执行。这个领域的研究正取得进展,垃圾收集器这些年已有改进。 届时,更好的算法会出现,从而提供更具确定性的行为。
早先我提及,数字处理代码通常不调用垃圾收集。对一些适度简单的应用来说确实如此,在这些应用程序里,主要涉及数字,也没有太多相关的内存分配。这其实取决于问题的本质 以及你已经设计出来的方案。如果它涉及许多生命期为中短期的对象,垃圾收集器将会被相当频繁地调用。如果只有少数长生命期对象,并且一直到应用程序结束时才释放,那么这些对象将被提升 为年长一代,并导致收集调用显著减少(如果有的话)。
figure 2 展示了一个没有调用垃圾收集器的执行矩阵乘法的应用程序。我选择矩阵是因为它们是现实世界里许多科学 计算应用程序的核心。矩阵提供了一种实用方式来解决许多应用领域的问题,例如在计算机图形算法、计算机 x 线断层摄影、遗传学、密码学、电力网和经济学领域。
figure 2 代码定义了一个matrix类,它声明一个二维数组用于存储矩阵数据。main方法创建 该类的三个实例,每个维度都是200×200(每个对象约313kb大小)。这些矩阵每一个引用以传值方式传递到 matmul 方法(引用本身以值方式传送而不是实际的对象),然后 matmul 方法执行矩阵 a 和 b 的乘法,并存储结果到矩阵 c。
为了更加有趣,matmul 方法在一个循环中被调用 1000 次。换句话说,我控制着这些对象的重用以有效地执行 1000 次“不同”矩阵的乘法运算而没有一次调用垃圾收集器。通过.net通用语言运行时的内存性能计数器, 你可以监视收集的次数。
然而,对于较大型的计算,如果你请求比可用内存更多的空间,垃圾收集最终不可避免。这种情形下,你可以二者择一。例如孤立代码中性能关系密切的代码,将之改为非受管代码,然后从c#受管代码中调用它们。这里一个警告是 p/invoke 或.net interop 调用会招致小的运行时开销,所以你可能将其作为最后一种选择,或者如果你确信运算的粒度足以能抵消调用所需的开销,就采用它。
垃圾收集功能不应该阻碍生成高性能科学计算代码。其目的是消除你用别的方式不得不面对的内存管理问题,只要你明白它的工作原理以及使用它所需的成本,你就不需要担心垃圾收集 的开销。
现在让我们离开 clr,转到语言本身。正如我早先提及,c#有许多特性使它十分适合于科学计算。下面让我们逐一讨论这些特性。  面向对象
面向对象
c#是一种面向对象语言。既然现实世界是由具有动态属性的密切相关的对象组成,那么面向对象程序设计方法常常是科学计算编程问题的最佳解决方案。 此外,通过替代内部代码片段,结构良好,面向对象的代码可以更容易被修改以适应科学计算模型的变化。
然而,不是所有科学计算问题都表现为类似对象的特性或关系,所以面向对象方法在处理此类问题时会导致不必要的复杂性。例如,figure 2 中 已有的矩阵乘法代码没有使用专门的类——在单个类中声明三个多维数组的矩阵。
问题可能涉及对象间复杂的关系,而对象的编程则带来进一步的复杂性或不必要的开销。以分子动力学(md)为例,分子动力学广泛应用于计算化学、物理学、生物学和材料科学。最早使用计算机 进行科学计算者之一要追溯到1957年,alder 和 wainwright 模拟了 150 个氩原子的运动。在md中,科学家感兴趣的是通过两个物体间的势模拟原子间的相互作用,这种 方式类似于行星、太阳、卫星和恒星之间受地心引力的影响而产生相互作用一样。采用面向对象方法建模两个原子间的相互作用可能不是一个坏想法。假设一个立方体内包含n3个原子,n为一个很大的数字。 能量守恒等式所产生的算术计算强度是如此之大,以致于借助传统的程序过程(非面向对象)来实现的话,必须进行过程简化和解决性能问题,也就是说,过程代码会 变得更复杂且性能更差。它真正取决于数据存储和所使用的算法。
你可以用 c# 来解决问题。使用语言所具备的强大的面向对象能力可能不是最佳选择,但它为传统的科学计算程序员提供了良好的开端。单个类可以包含用于执行计算和产生结果的 所有变量和方法。尽管如此,对于相对较大的问题,由于 oop 提供的模块化和数据完整性,它对科学计算编程来说是个很有价值的工具,这使代码扩充和重用变得 更容易。  高精度浮点运算
高精度浮点运算
没有哪个科学计算代码能忽视精确度和准确度。即使现今最强大的计算机也只能运算有限位数精度,具备更高的精度将有助于获取更准确结果。这方面的重要性不能低估,由于计算机算术运算错误而导致的灾难会让你清楚地认识这一点,例如,1996 年著名的 ariane 5号非载人火箭爆炸(其惯性参照系统里一个64位浮点数被错误转换为16位有符号整数……嘣)。当然,你或许不会开发火箭软件,但重要的是必须知道在许多科学计算应用程序中高精度的重要性以及为什么如此重要,同时,用于二进制浮点算法的 ieee 754 标准 与其说有所帮助,不如说实际的约束更多些。
c#允许浮点算术使用更高的硬件平台支持的精度,譬如 intel 的 80 位双精度格式。这种扩展类型具有比双精度类型更高精度,它被底层硬件执行所有浮点算术时隐式使用,这样提供了准确 的或近似准确的结果。下面这段话直接摘录于 c# 规格说明书第 4.1章节,以此作为 c# 支持高精度浮点运算的例子:
……在形如 x*y/z 的表达式中,乘法产生超出双精度取值范围的结果,但是接着除法又使临时结果回到双精度取值范围里,表达式的事实上的结果是在更高精度范围内被求值,所产生的是有穷结果而不是无穷大。
c#也支持十进制类型——128位数据类型,适合于金融和货币计算。  值类型,或轻量级对象
值类型,或轻量级对象
c#中对象类型主要有两种——引用类型(重量级对象)和值类型(轻量级对象)。
引用类型总是在堆中分配(除非使用 stackalloc 关键字),并给予一个额外的间接层;也即,它们需要通过对其存储位置的引用来访问。既然这些类型不能直接访问, 某个引用类型的变量总是保存实际对象的引用(或 null ) 而不是对象本身。假设引用类型在堆中分配,运行时必须确保每个分配请求被正确执行。考虑下面代码,它执行一次成功的分配:
matrix m = new matrix(100, 100);其幕后执行是:clr内存管理器收到分配请求,它会计算存储该对象包括头部和类变量所需的内存数量。然后内存管理器检查堆中可用空闲空间,以确认是否有足够空间供这次分配。如果有,对象 所需空间会被成功分配并且对其存储地址的引用也会被返回。如果没有足够空间存储对象,垃圾收集器将被启动去释放一些空间并进行堆紧缩操作。
class point{ private double x, y; public point (double x, double y) { this.x = x; this.y = y; }} 这个类的一个实例占用24字节,其中8字节用于对象头,剩余16字节用于两个双精度变量x和y。与此同时,引用类型是包含在值类型对象中的(例如,结构中包含数组) ,它不会导致整个对象在堆中分配。只有数组在堆中分配,对该数组的引用被置于在栈中存放的结构中。  复数算术
复数算术 z = x + yi, where i2 = -1复数在科学计算应用中广泛使用,用于研究物理现象,譬如涉及障碍的电流、波长和液体流动,分析汽车减震器的桁条压力、移动,发电机和电动机的设计,建模中大矩阵的的处理。它们形成这个宇宙中几乎任何事的基本等式,所以将复数视作编程语言中 单独一种数据类型对于许多科学计算应用来说是至关重要的。
c3 = c1 * c2 + 5 * (c1-13)如果此表达式以方法调用形式编写,你会得到类似下行代码:
complex c3 = c1.multiply(c2).add((c1.minus(13)).multiply忘记其中任何一处的括号,你将陷入在屏幕上查找编译错误。想象一下编写一个比上面表达式更复杂的数字表达式将会怎样。或者想象一段时间后重新回到你的代码,并打算在一个嵌套 了无数个add和multiply方法名的表达式中将“add”方法名改为“multiply”。首先你必须理解代码是做什么的,然后,如果幸运的话,经过多次不成功的修改尝试后你终于得到正确结果。运算符重载允许你以自然、合乎逻辑 的方式来表示数字表达式。
 多维数组
多维数组 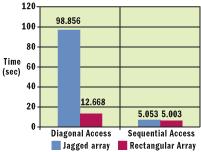
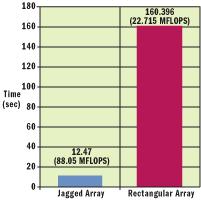
double[] myarray = new double[row_dim * column_dim];要索引这个数组的元素,使用下列偏移:
myarray[row * column_dim + column];这勿庸置疑比等价的不规则或矩形数组快。
 不安全方法
不安全方法 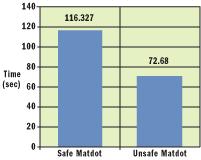
 语言互用性
语言互用性 基准测试(benchmarks)
基准测试(benchmarks) 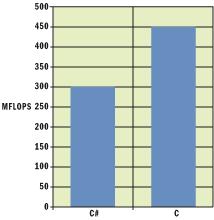
 结束语
结束语 新闻热点
疑难解答