Origin绘制三维图怎么绘制垂线和误差棒?

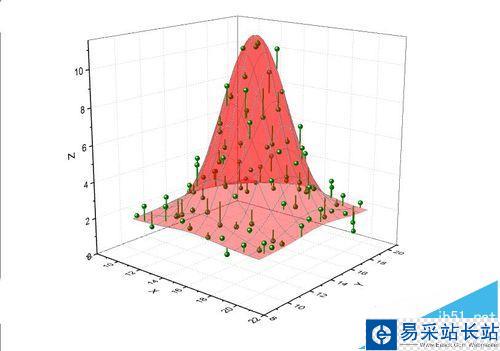
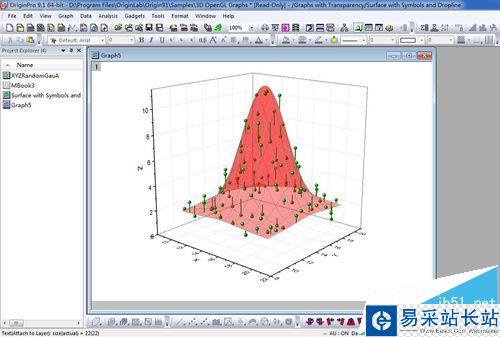
在三维图中的数据处理中通常有一个目标函数，计算数据或是试验结果与目标函数通常有些差距，为了更方便表明实际数据与目标函数的关系，我们可以在实验数据与目标函数之间用垂线进行关联。在这篇经验中，我们的目标函数所在平面是高斯平面，通过Drop lines（垂线）和error bars(误差棒）构建实际数据与目标函数的关系。如图为最终效果图。

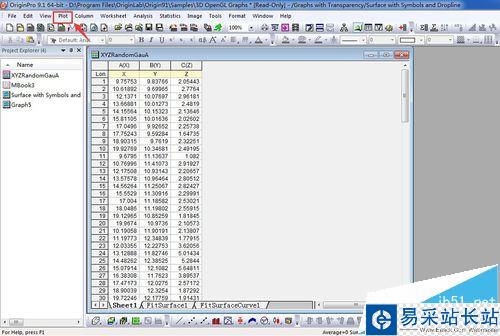
1、激活如图所示的worksheet为三维散点图的初始数据，选中XYZ数据执行Plot-3D Symbol/Bar/Vector-3D Scatter。

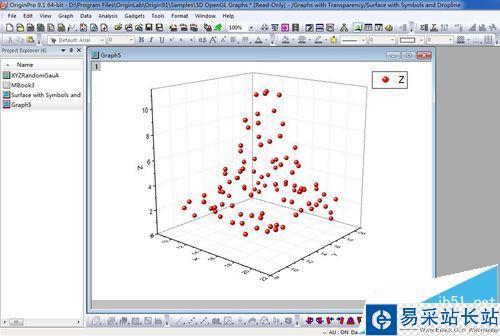
2、得到如图所示的三维散点图。

3、现在讲3D Color Fill Surface添加到3D scatter中，双击图层1可以打开Layer Contents对话框，如图所示。

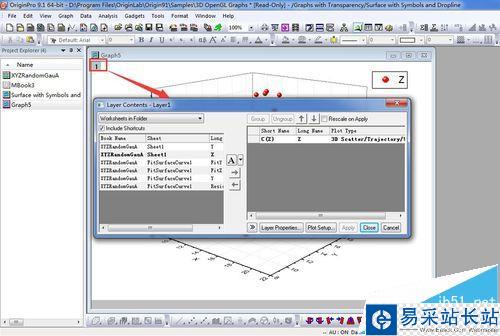
4、在Layer Contents中，选择Matrices in Folder。在左侧选择三维表面图所在的矩阵，添加到右侧，并点击图中A，选择3D-Surface。

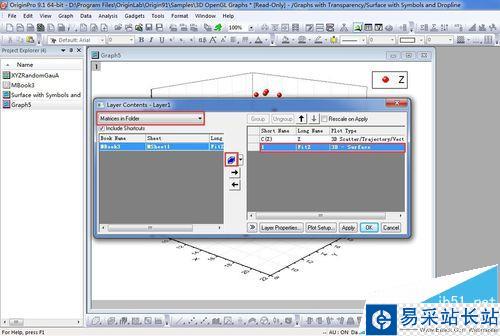
5、点击OK，得到如图所示的图形。

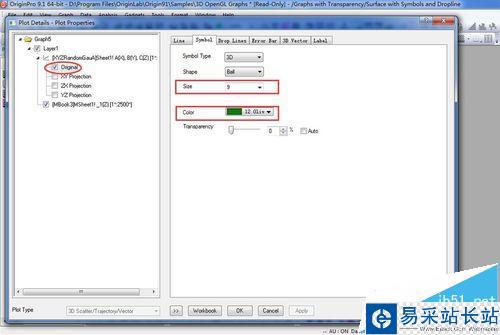
6、双击图形打开Plot Details，在左侧选择如图所示的Original，在右侧选择Symbol选项，将形状修改为Ball,将Size大小设置为9，颜色设置为Olive。

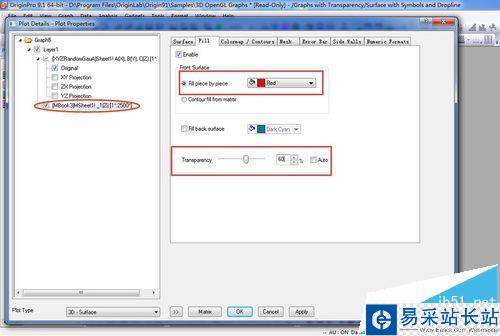
7、在左侧选择表面图所在Matrix，选择右侧的Fill选项（如图），将Front Surface中Fill Piece by Piece的颜色Red，将透明度修改为60%。

8、选择右侧Mesh选项，将Line Width修改为1，并Set Total Number of Majors为X=9和Y=9.

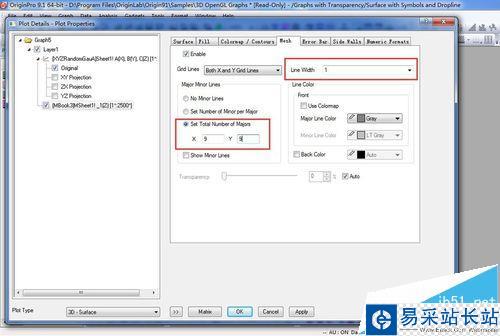
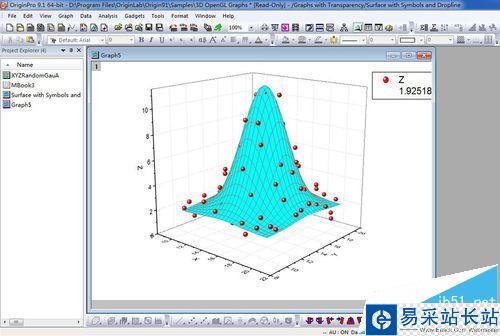
9、现在我们来绘制垂线，在左侧如图选择三维散点图的Original，选择Drop Lines选项，设置Parallel to Z Axis，勾选Drop to Surface。将drop line的Width设置为2，将Color设置为Auto。

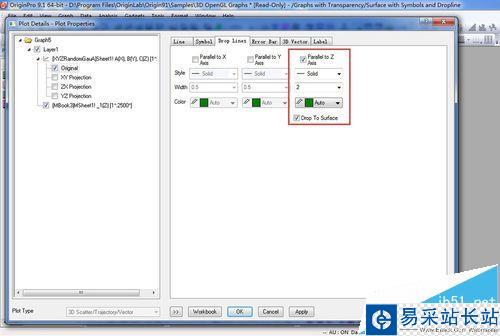
10、点击OK，最终效果图如图所示。

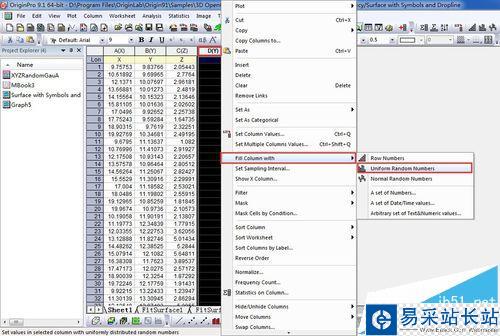
11、下面顺便介绍下，在三维表面图插入误差棒的效果，步骤1-7一样，不同的是初始数据中，选择D列右击选择Fill Column with，点击Uniform Random Numbers。

12、双击图片打开Plot Details，在三维散点图的Original中选择error bar选项，选择Col（D）为Z Error值。